$l$ લંબાઇની રેખા પર $q$, $Q$ અને $4q$ વિદ્યુતભારને એક છેડાથી અનુક્રમે $0,\,\frac {l}{2}$ અને $l$ અંતરે મૂકેલા છે. જો વિજભાર $q$ પર લાગતું બળ શૂન્ય કરવું હોય તો $Q$ વિજભાર કેટલો હોવો જોઈએ?
Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 2ઊગમબિંદુ આગળ $0.009\ \mu C$ નો બિંદુવત વિદ્યુતભાર મૂકેલો છે. બિંદુ $(\sqrt 2 ,\,\,\sqrt 7 ,\,\,0)$ આગળ આ બિંદુવત વિદ્યુતભારને લીધે વિદ્યુતક્ષેત્રની તીવ્રતાની ગણતરી કરો.View Solution
- 3$R$ ત્રિજ્યાનો એક ગોળો છે અને $2R$ ત્રિજ્યાનો બીજો કાલ્પનિક ગોળો કે જેનું કેન્દ્ર આપેલ ગોળાના કેન્દ્રને સુસંગત છે. જેના પરનો વિદ્યુતભાર $q$ છે. કાલ્પનિક ગોળા સાથે સંકળાયેલ ફલક્સ ........ છે.View Solution
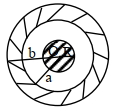
- 4આકૃતિમાં દર્શાવ્યા પ્રમાણે અંદરની ત્રિજયા $a$ અને બહારની ત્રિજયા $b$ ધરાવતા ગોળીય કવચની અંદર $R$ ત્રિજયા અને $q$ વિદ્યુતભાર ધરાવતો ધાતુનો ગોળો છે. તો વિદ્યુતક્ષેત્ર $\overrightarrow{{E}}$ વિરુદ્ધ તેના કેન્દ્ર $O$ થી અંતર $r$ સાથેનો ગ્રાફ લગભગ કેવો મળશે?View Solution
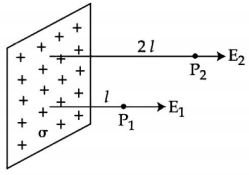
- 5આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરોView Solution
- 6View Solutionગાઉસનો નિયમ કઈ પ્રણાલી માટે વિદ્યુતક્ષેત્રની સરળ ગણતરીમાં મદદ કરે છે ?
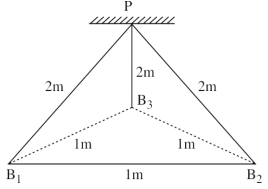
- 7ત્રણ દરેક $2 \,C$ જેટલા વિદ્યુતભારીત બોલને $2 \,m$ લંબાઈના સ્લિકના દોરાથી (આકૃતિમાં દર્શાવ્યા અનુસાર) સમાન બિંદુ $P$ આગળથી લટકાવવામાં આવ્યા છે. તેઓ $1 \,m$ બાજુનો સમબાજુ ત્રિકોણ બનાવે છે. વિદ્યુતભારીત બોલ પર લાગતુ કુલ બળ અને કોઇપણ બે વિદ્યુતભારો વચ્યે પ્રવર્તતા બળોનો ગુણોત્તર .......... થશે.View Solution
- 8View Solutionએક ધન વિદ્યુતભારીત લોલક ઉપર તરફના એકરૂપ વિદ્યુતક્ષેત્રમાં દોલન કરે છે. તેનો આવર્તકાળ જ્યારે તે વિદ્યુતક્ષેત્ર વગર દોલન કરે તેની સરખામણીમાં
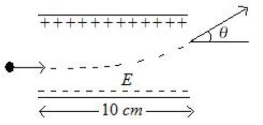
- 9બે સમાંતર પ્વેટ (તક્તિ)ની વચ્યે $10\,N/C$ નું નિયમિત વિદ્યુતક્ષેત્ર ઉત્પન્ન થાય છે. એક ઇલેક્ટોન $0.5\,eV$ ગતિઊર્જા સાથે તક્તિઓની વચ્યેના વિસ્તારમાં સંમિતિ પૂર્વક દાખલ થાય છે. દરેક તક્તિઓની લંબાઈ $10\,cm$ છે. જ્યારે ઈલેકટ્રોન આ ક્ષેત્રના વિસ્તારમાંથી બહાર નીકળે ત્યારે તેના ગતિપથના વિચલન કોણ $(\theta)$ $...........^{\circ}$ (ડિગ્રી) થશે.View Solution
- 10એક બંધ પૃષ્ઠની અંદર અને બહાર જતું વિદ્યુત ફલ્કસ ${\varphi _1}$ અને ${\varphi _2}$ છે.તો પૃષ્ઠની અંદર વિદ્યુતભાર કેટલો હશે?View Solution