$LR$-પરિપથમાં ઇન્ડિકટીવ રીએકટન્સ અવરોધ $R$ જેટલો છે,પરિપથમાં લગાવેલ વોલ્ટેજ $E = {E_0}\cos (\omega t)$ હોય, તો પાવર કેટલો થાય?
Medium
Download our app for free and get started
c
(c) \(P = {E_{rms}}{i_{rms}}\cos \phi = \frac{{{E_0}}}{{\sqrt 2 }} \times \frac{{{i_0}}}{{\sqrt 2 }} \times \frac{R}{Z}\)
==> \(\frac{{{E_0}}}{{\sqrt 2 }} \times \frac{{{E_0}}}{{Z\sqrt 2 }} \times \frac{R}{Z}\)\( \Rightarrow \,\,P = \frac{{E_0^2R}}{{2{Z^2}}}\)
Given \({X_L} = R\) so, \(Z = \sqrt 2 R\)\( \Rightarrow \,P = \frac{{E_0^2}}{{4R}}\)
(c) \(P = {E_{rms}}{i_{rms}}\cos \phi = \frac{{{E_0}}}{{\sqrt 2 }} \times \frac{{{i_0}}}{{\sqrt 2 }} \times \frac{R}{Z}\)
==> \(\frac{{{E_0}}}{{\sqrt 2 }} \times \frac{{{E_0}}}{{Z\sqrt 2 }} \times \frac{R}{Z}\)\( \Rightarrow \,\,P = \frac{{E_0^2R}}{{2{Z^2}}}\)
Given \({X_L} = R\) so, \(Z = \sqrt 2 R\)\( \Rightarrow \,P = \frac{{E_0^2}}{{4R}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionકેપેસિટરમાં કયાં પ્રવાહનું વહન થતું નથી?
- 2$27\; mH$ ઇન્ડક્ટર સાથે $30\; \mu \,F$ નું સંપૂર્ણ વિદ્યુતભારિત કેપેસીટર જોડેલ છે. તો પરિપથમાં થતાં મુક્ત દોલનોની કોણીય આવૃત્તિ કેટલી હશે?View Solution
- 3$100\,\Omega$ અવરોધનો અવરોધક, $1\,H$ ઈન્ડકટન્સનો ઈન્ડકટર અને $6.25\,\mu F$ કેપેસીટન્સ (સંધારકતા) નો સંધારક (કેપેસીટર) એસી ઉદગમ સાથે શ્રેણીમાં જોડેલા છે. પરિપથનો કવોલીટી અવયવ ......... હશે.View Solution
- 4ઓસીલેટર પરિપથનો કેપેસીટર એક બંધ પાત્રમાં છે. જ્યારે પાત્રને ખાલી હોય ત્યારે પરિપથ $10\, kHz$ ની આવૃતિથી અનુનાદ કરે છે. જ્યારે પાત્રને વાયુ વડે ભરી દેવામાં આવે ત્યારે તે તેની અનુનાદિત આવૃતિ $50\, Hz$ મળે છે. તો આ વાયુનો ડાઈઇલેક્ટ્રિક અચળાંક કેટલો હશે?View Solution
- 5$50\,Hz$ આવૃતિ એ $30\,ohm$ અવરોધ અને $20\,ohm$ ઇન્ડક્ટીવ રીએક્ટન્સ કોઇલને $200\,volt$, $100\,Hz$ આવૃતિવાળા ઉદગમ સાથે જોડતા પ્રવાહ ....... $A$View Solution
- 6$LCR$ ઓસ્સિલેટર પરિપથમાં અનુનાદ સમયે ઇન્ડકટરમાં સંગ્રહિત ઊર્જા શોધો. જો ઉદગમનાં વૉલ્ટેજ $10\,V$ અને અવરોધ $10\, \Omega$ અને ઇન્ડકટર $=1 H$ છે ($J$ માં)View Solution
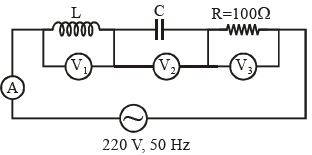
- 7આકૃતિમાં દર્શાવેલ પરિપથમાં વોલ્ટમિટર $V_1$ અને $V_2$ એ $300 \;V $ દર્શાવે છે. વોલ્ટમીટર $V_3$ અને એમિટર $A$ નું રીંડિંગ અનુક્રમે કેટલું થાય?View Solution
- 8$LCR$ શ્રેણી પરિપથમાં $R = X_L = 2X_C$ હોય,તો ઇમ્પિડન્સ અને પ્રવાહ અને વોલ્ટેજ વચ્ચે કળા તફાવત કેટલો થાય?View Solution
- 9$A.C.$ નું $D.C.$ માં રૂપાંતર કરવાની પ્રક્રિયાને શું કહેવાય?View Solution
- 10$0.5\,mH$ ના ઈન્ડકટર, $20\,\mu F$ નો સંધારક, અને $20\,\Omega$ ના અવરોધને $220\,V$ ના $ac$ ઉદગમ સાથે શ્રેણીમાં જોડવામાં આવે છે. જો પ્રવાહ $emf$ સાથે કળામાં હોય, તો પરિપથમાં પ્રવાહનો કંપવિસ્તાર $\sqrt{x} \, A$ મળે છે. $x$ નું મૂલ્ય $.............$ થશે.View Solution