\(\overrightarrow{ v }_{01}=(\sqrt{3 \hat{ i }}+\hat{ j }) m / s\)
\(\overrightarrow{ v }_{02}=\overrightarrow{0}\)
\(m _{1}=2 m _{2}\)
After collision, \(\overrightarrow{ v }_{1}=(\hat{ i }+\sqrt{3} \hat{ j }) m / s\)
\(\overrightarrow{ v }_{2}=?\)
Applying conservation of linear momentum,
\(m _{1} \overrightarrow{ v }_{01}+ m _{2} \overrightarrow{ v }_{0 2}= m _{1} \overrightarrow{ v }_{1}+ m _{2} \overrightarrow{ v }_{2}\)
\(2 m_{2}(\sqrt{3 \hat{i}}+\hat{j})+0=2 m_{2}(\hat{i}+\sqrt{3} \hat{j})+m_{2} \vec{v}_{2}\)
\(\overrightarrow{ v }_{2}=2(\sqrt{3 \hat{ i }}+\hat{ j })-2(\hat{ i }+\sqrt{3} \hat{ j })\)
\(=2(\sqrt{3 \hat{1}}-\hat{j})+2(\hat{i}-\sqrt{3} \hat{j})\)
\(\overrightarrow{ v }_{2}=2(\sqrt{3}-1)(\hat{ i }-\hat{ j })\)
for angle between \(\overrightarrow{ v }_{1} \& \overrightarrow{ v }_{2}\)
\(\cos \theta=\frac{\overrightarrow{ v }_{1} \cdot \overrightarrow{ v }_{2}}{\overrightarrow{ v }_{1} \overrightarrow{ v }_{2}}=\frac{2(\sqrt{3}-1)(1-\sqrt{3})}{2 \times 2 \sqrt{2}(\sqrt{3}-1)}\)
\(\cos \theta=\frac{1-\sqrt{3}}{2 \sqrt{2}} \Rightarrow \theta=105^{\circ}\)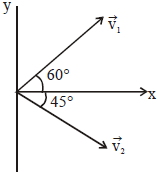
Download our appand get started for free
Similar Questions
- 1એક ખેલાડી $150 \mathrm{~g}$ દળના અને $20 \mathrm{~m} / \mathrm{s}$ ના દર (ઝડપ)થી ગતિ કરતા બોલને પકડે છે. જો આ કેચ પકડવાની પ્રક્રિયા $0.1$ sમાં પૂર્ણ થાય તો બોલ દ્વારા ખેલાડીના હાથ પર લાગતું બળ (મૂલ્ચમાં). . . . . .હશે.View Solution
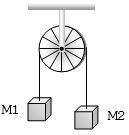
- 2$M_1$ અને $M_2$ નાં બે દળોને હલકી ખેંચાણ ન અનુભવતી દોરી કે જેને ધર્ષણાહિત પુલી પરથી પસાર કરવામાં આવી છે તેના બે છેડા આગળ બાંધવામાં આવેલા છે. જ્યારે દળ $M_2$ એ $M_1$ કરતા બમણું હોય ત્યારે તંત્રમાં $a_1$ જેટલો પ્રવેગ મળે છે.જ્યારે $M_2$ એ $M_1$ કરતા ત્રણ ગણું હોય છે ત્યારે તંત્રનો પ્રવેગ $a_2$ જેટલો મળે છે. $\frac{a_1}{a_2}$ ગુણોત્તર શોધો.View Solution
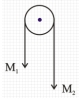
- 3એક ખોખાંની અંદર $M$ જેટલું દળ ધરાવતું ચોસલું '$a$' જેટલા પ્રવેગથી નીયે તરફ ગતિ કરે છે. ચોસલું બોક્ષના તળિયા ઉપર તેના વજન કરતા યોથા ભાગનું બળ લગાડે છે. $'a'$ નું મૂલ્ય ............ હશે.View Solution
- 4View Solutionરોકેટ નીચેની પૈકી કોના સંરક્ષણના નિયમ પર કાર્ય કરે છે?
- 5લીફ્ટમાં ઉભેલો માણસના હાથમાંથી એક સિક્કો પડે છે.જો લિફ્ટ સ્થિર હોય તો તેને નીચે પડતાં $t_{1}$ સમય લાગે છે અને જો લિફટ અચળ ગતિ કરતી હોય તો તેને નીચે પડતાં $t_{2}$ સમય લાગતો હોય તો ....View Solution
- 6દોરડા પર કેટલા લઘુત્તમ પ્રવેગથી ઉતરી શકાય જો દોરડાની તણાવ ક્ષમતા માણસના વજન કરતાં $\frac{2}{3}$ ગણી હોય?View Solution
- 7એક $300 kg$ ટ્રોલીમાં $25 kg$ ની રેતી ભરેલી બેગ સાથે $27 km/hr $ ની નિયમિત ઝડપે ઘર્ષણ રહિત ટ્રેક પર ગતિ કરે છે. થોડાં સમય બાદ બેગમાંથી રેતી $0.05 kg/s$ ના દરથી નીકળીને ટ્રોલીના તળિયે પડે છે. રેતીની બેગ સંપૂર્ણ પણે ખાલી થઈ જાય ત્યારે ટ્રોલીની ઝડપ .....$km/hr$ શોધો.View Solution
- 8View Solutionનીચેનામાથી કયો બળો માટે ક્રમ સાચો છે?
- 9માલગાડીમાં ખુલ્લો ડબ્બો $10 \,m / s$. નાં નિયમિત વેગ સાથે ગતિ કરી રહ્યું છે. જો વરસાદ $5 \,kg / s$ ની દરે શૂન્ય વેગ સાથે પાણી ઉમેરતો હોય, તો પછી ગાડીના સમાન વેગને જાળવવા માટે એન્જિન દ્વારા પુરું પાડવામાં આવતું જરુરી વધારાનું બળ ............ $N$ છે.View Solution
- 10વજનરહિત અને ઘર્ષણરહિત ગરગડીમાંથી પસાર થઈને વજનહીન તાર સાથે ${m_1}$ અને ${m_2}$ (ઊભી) દળના બે બ્લોકને જોડેલા છે. જો તંત્રનો પ્રવેગ $\left( {\frac{g}{8}} \right)$ હોય, તો દળનો ગુણોત્તર કેટલો હશે?View Solution