પ્રારંભ માં \(\,{\text{k}}\ell \,\, = \,\,{\text{Mg}}\,\, \Rightarrow \,\,{\text{k}}\,\, = \,\,\frac{{{\text{5}}\,\, \times \,\,{\text{10}}}}{{{\text{0}}{\text{.1}}}}\,\, = \,\,500\,\,N/m\)
ધારો કે તે ઊંચાઈ સુધી જતો હોય ત્યારે સ્પ્રિંગમાં થતું સંકોચન \(\,{\text{(h}}\,\,{\text{ - }}\,\,\ell {\text{)}}\)
ઉર્જા સરક્ષણ ના નિયમ પરથી, \(\,\,\frac{{\text{1}}}{{\text{2}}}\,\,M{v^2}\, + \,\,\frac{1}{2}\,K{\ell ^2}\, = \,\,Mgh\,\, + \,\,\frac{1}{2}\,\,K\,{(h\,\, - \,\,\ell )^2}\)
\( \Rightarrow \,\,\,M{v^2}\, + \,\,K\,[{\ell ^2}\, - \,\,{(h\,\, - \,\,\ell )^2}]\,\, = \,\,2Mgh\,\, \Rightarrow \,\,M{v^2}\, + \,\,K\,[h(2\ell \,\, - \,\,h)]\,\, = \,\,2mgh\)
\( \Rightarrow \,\,20\,\, + \,\,500\,[h(0.2\, - \,\,h)]\,\, = \,\,100\,h\,\, \Rightarrow \,\,1\,\, + \,\,25\,\,(0.2h\, - \,\,{h^2})\,\, = \,\,5h\)
\( \Rightarrow \,\,\,1\,\, + \,\,5h\,\, - \,25{h^2}\, = \,\,5h\,\, \Rightarrow \,\,{h^2}\, = \,\,\frac{1}{{25}}\,\, \Rightarrow \,\,h\,\, = \,\,\frac{1}{5}\,\, = \,\,0.2\,m\)
Download our appand get started for free
Similar Questions
- 1$m = 10\,kg$ દળનો એક બ્લોક સમક્ષિતિજ ટેબલ પર સ્થિર પડેલો છે. બ્લોક અને ટેબલ વચ્ચે નો ઘર્ષણાંક $0.05$ છે.જ્યારે $50\,g$ દળ ધરાવતી એક બુલેટ $v$ વેગથી બ્લોકમાં ઘૂસે છે, તેથી બ્લોક ટેબલ પર $2\,m$ અંતર કાપીને સ્થિર થાય છે.જો મુક્ત પતન કરતા પદાર્થને $\frac {v}{10}$ વેગ જાળવવો હોય તો ઉર્જાના વ્યયને અવગણતા અને $g=10\,ms^{-2}$ લેતા $H$ ની કિંમત ................... $\mathrm{km}$ થશે?View Solution
- 2View Solutionઊર્જા સંરક્ષણનો નિયમ શું નિર્દેંશ કરે છે?
- 3View Solutionએક દડો જમીન પર અથડાઇને અસ્થિતિસ્થાપક સંઘાત બાદ ઉછળે છે. આ કિસ્સામાં.....
- 4એક $m$ દળની ગોળીને $u$ વેગથી સમક્ષિતિજ દિશામાં છોડવામાં આવે છે. આ ગોળી ટ્રકમાં રહેલી રેતીની થેલીમાં ઘુસી જાય છે. જો ટ્રકનું દળ $m$ હોય તો સંઘાત પછી ટ્રકનો વેગ કેટલો હશે ?View Solution
- 5$10\,kg$ દળનો એક બ્લોક $x$-અક્ષ પર $F=5 x\,N$ બળની અસર હેઠળ છે. આ બળ વડે બ્લોકને $x=2\,m$ થી $4\,m$ સુધી ગતિ કરવા માટે કરવું પડતું કાર્ય ...... $J$ હશે.View Solution
- 6$m $ દળનો ગોળા $u$ વેગથી ગતિ કરીને $m$ દળના સ્થિર ગોળા સાથે સંઘાત અનુભવે છે.જો રેસ્ટિયુશન ગુણાંક $\frac{1}{2}$ હોય તો પ્રથમ ગોળાની અંતિમ અને શરૂઆતના વેગનો ગુણોતરView Solution
- 7$1500N/m$ અને $ 3000 N/m$ બળઅચળાંક ધરાવતી સ્પિંગ્ર પર સમાન બળ લગાવતા સ્થિતિઊર્જાનો ગુણોત્તર કેટલો થાય?View Solution
- 8એક માણસની ગતિઊર્જા તેનાથી અડઘું દળ ઘરાવતા છોકરાથી અડઘી છે.જો માણસની ઝડપમાં $ 1 m/s$ નો વઘારો કરવામાં આવે તો બંનેની ગતિઊર્જા સમાન થાય છે. માણસની મૂળ ઝડપView Solution
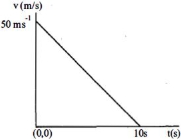
- 9$10\, kg$ દળના એક પદાર્થ માટે વેગ-સમયનો આલેખ આકૃતિમાં દર્શાવેલો છે. ગતિની પ્રથમ બે સેકન્ડ દરમ્યાન પદાર્થ પર થયેલ કાર્ય કેટલા .............. $\mathrm{J}$ હશે?View Solution
- 10View Solutionએક ધાતુનો બોલ દિવાલને પટકાઈ છે અને પાછો ફરતો નથી. જ્યારે એક તેટલા જ દળનો રબ્બરનો બોલ સમાન વેગથી પટકાઈને પાછો ફરે છે. આ પરથી શું તારણ કાઢી શકાય?
