$m$ દળ અને $2\, v$ વેગ ધરાવતો પદાર્થ તે જ દિશામાં જતાં $2\,m$ દળ અને $v$ વેગથી ગતિ કરતા પદાર્થ સાથે અથડાય છે. અથડામણ પછી પ્રથમ પદાર્થ ઊભો રહી જાય છે છે જ્યાંરે બીજો પદાર્થ બે $m$ દળના પદાર્થમાં વિભાજિત થાય છે.જે શરૂઆતની દિશા સાથે $45^o$ ના ખૂણે ગતિ કરે તો ગતિ કરતાં દરેક પદાર્થનો વેગ કેટલો હશે?
JEE MAIN 2019, Medium
Download our app for free and get started
b
Linear momentum conservation
Linear momentum conservation
\(m\) \(2v + 2m v = m \)\( \times \,0 + m\frac{{v'}}{{\sqrt 2 }} \times 2\)
\(v' = 2\sqrt 2 \,v.\)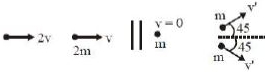
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
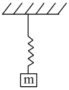
- 1View Solutionસ્પ્રિંગ શરૂઆતમાં મૂળ સ્થિતિમાં છે, જ્યારે બ્લોકને મુક્ત કરવામાં આવે ત્યારે સ્પ્રિંગમાં મહતમ કેટલું તણાવબળ ઉત્પન્ન થશે?
- 2View Solutionએક દડો જમીન પર અથડાઇને અસ્થિતિસ્થાપક સંઘાત બાદ ઉછળે છે. આ કિસ્સામાં.....
- 3$ 2.05 \times {10^6}\;kg $ દળ ધરાવતી ટ્રેનનો વેગ $5\; min$ માં $ 5\;m/s $ થી $25\; m/s $ થાય છે,તો એન્જિનનો પાવર કેટલા ......... $MW$ હશે?View Solution
- 4એક માધ્યમમાં $m= 10^{-2}$ $kg$ દળનો એક પદાર્થ ગતિ કરે છે,જે $F= -kv^2$ નો ઘર્ષણબળ અનુભવે છે.તેની પ્રારંભિક ઝડપ $v_0= 10$ $ms^{-1}$ છે.જો $10$ $s$ પછી તેની ઊર્જા $\frac{1}{8}$ $mv_0^2$ છે,તો $k$ નું મૂલ્યView Solution
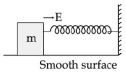
- 5$'m'$ દળ ધરાવતો અને $E$ જેટલી ગતિઊર્જા ધરાવતો બ્લોક (ચિત્રમાં દર્શાવ્યા અનુસાર), જ્યારે તેની ઝડપ અડધી થાય ત્યારે સ્પ્રિંગને $25\;cm$ અંતર સુધી દબાવે છે. વપરાયેલ સ્પ્રિંગ માટે સ્પ્રિંગ અચાળાંક $nE \;Nm ^{-1}$ મળે છે. $n$ નું મૂલ્ય ......... હશે.View Solution
- 6$m_1$ અને $m_2$ દળના બે સમકડાના ગાડા વચ્ચે એક સ્પ્રિંગ સંકોચાયેલી છે. જ્યારે રમકડાના ગાડાને મુક્ત (છોડવામાં) કરવામાં આવે ત્યારે દરેક ગાડા પર આવેલી સ્પ્રિંગ સમાન સમય $t$ માટે સમાન મૂલ્યનું અને પરસ્પર વિરૂદ્ધ દિશામાં બળ લગાડે છે. જો જમીન અને ગાડા વચ્ચેનો ઘર્ષણ ગુણાંક $\mu$ સમાન હોય તો બે રમકડાના ગાડાઓના સ્થાનાંતરનો ગુણોત્તર શોધો.View Solution
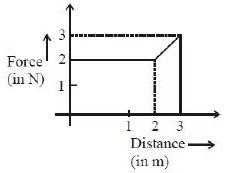
- 7ગ્રાફમાં દર્શાવ્યા પ્રમાણે એક કણ આપેલ સ્થાન સાથે બદલાતા બળના કારણે એક પારિમાણિક ગતિ કરે છે. $3\, m$ ગતિ કર્યા પછી કણની ગતિઉર્જા કેટલા .............. $\mathrm{J}$ થશે?View Solution
- 8સમતલ ખરબચડા રોડ પર $500\,kg$ દળ ધરાવતી બસને $4\,km$ અંતર સુધી $80\,km / h$ ની ઝડપ જાળવી રાખવા માટે બસના એન્જિન વડે કરવું પડતું કાર્ય $......\,kJ$ થાય. [બસના ટાયર અને રોડ વચ્યેનો ધર્ષણાંક $0.04$ છે.]View Solution
- 9પ્રારંભમાં સ્થિર પદાર્થ $2M $ અને $3M $ દળ ના બે ટૂકડામાં વહેંચાય છે અને તેમની બંનેની મળીને કુલ ગતિઊર્જા $E$ છે. ટૂકડામાં વહેંચાયા બાદ $ 2M$ દળના ટૂકડાની ગતિઊર્જા કેટલી હશે?View Solution
- 10$10\,s$ માં $100 \,m$ ઊંચાઈ સુધી $500 \,kg$ પાણીને પંપ કરી શકે એવા પંપનો પાવર ........... $kW$ છે...View Solution