$m$ દળ અને $A$ આડછેદ ધરાવતા લંબઘન બ્લોક $\rho$ ઘનતા ધરાવતા પ્રવાહીમાં તરે છે, તેને સમતોલન સ્થિતિમાંથી સૂક્ષ્મ શિરોલંબ સ્થાનાંતર કરાવતા તેની સરળ આવર્તગતિનાં આવર્તકાળ $T$ હોય તો ...
AIIMS 2018, Diffcult
a
\(M g=A l \rho g \Rightarrow m=A \rho l\)
\(M g=A l \rho g \Rightarrow m=A \rho l\)
Where, \(l=\) length of part immersed in liquid.
When it is given in downward displacement \(y\), restoring force (upward direction) on block is
\(F=-[A(l+y) \rho g-m g]\)
\(=-[A(l+y) \rho g-A l \rho g]\)
\(=-A \rho g y\)
i.e. \(F \propto-y\) or \(a \propto-\gamma,\) so it execute SHM (inertia factor). Mass of block \(=m\)
Spring factor \(=A \rho g\)
Time period \(=2 \pi \sqrt{\frac{\text { Inertia factor }}{\text { spring factor }}}\)
\(T=2 \pi \sqrt{\frac{m}{A \rho g}}\)
\(\Rightarrow T^{2} \propto \frac{m}{A \rho}\)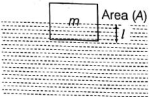
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$LCR$ પરિપથ એ અવમંદિત દોલકને સમતુલ્ય છે.નીચે દર્શાવ્યા મુજબ સંઘારક ને $Q_0$ જેટલા વિદ્યુતભારથી વીજભારિત કરેલ છે.અને ત્યારબાદ તેને $L$ અને $R$ સાથે જોડવામાં આવે છે. જો વિદ્યાર્થી, બે જુદાં-જુદાં $L_1$ અને $L_2$ $(L_1 > L_2)$ મૂલ્યોના ઇન્ડકટર માટે સંઘારક પરના મહત્તમ વિદ્યુતભારના વર્ગ $( Q^2_{max})$ વિરુદ્વ સમય માટેના ગ્રાફ દોરે,તો નીચે આપેલમાંથી કયો ગ્રાફ તેને સાચી રીતે રજૂ કરશે? (આકૃતિ રેખાકૃતિ છે અને તે એક જ સ્કેલ પર દોરેલ નથી. )View Solution
- 2View Solutionસરળ આવર્ત ગતિ કરતાં કણની મહત્તમ સ્થિતિઊર્જા અને મહત્તમ ગતિઊર્જાના સ્થાન વચ્ચેનું અંતર કેટલું હોય?
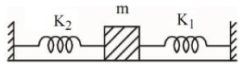
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે $m$ દ્રવ્યમાનને બે દોરી વચ્ચે લગાવેલ છે. બે સ્પ્રિંગોના સ્પ્રિંગ અચળાંક $K_1$ અને $K _2$ છે. ઘર્ષણ મુકત સપાટી પર $m$ દળના દોલનનો આવર્તકાળ છે.View Solution
- 4જ્યારે સરળ આવર્ત ગતિ કરતાં પદાર્થની સ્થિતિઊર્જા દોલન દરમિયાન તેના મહત્તમ મૂલ્યના ચોથા ભાગની થાય, ત્યારે સમતોલન સ્થાનથી સ્થાનાંતર તેના કંપવિસ્તાર $a$ ના પદમાં કેટલું હશે?View Solution
- 5બળપ્રેરિત દોલનોમાં કણનો કંપવિસ્તાર બળની $\omega_{1}$ આવૃતિ માટે મહત્તમ, જ્યારે બળની $\omega_{2}$ આવૃતિ માટે ઉર્જા મહત્તમ હોય, તોView Solution
- 6$S.H.M$ (સ.આ.ગ.) કરતા કણ માટે સ્થાનાંતર $x=10 \sin \left(w t+\frac{\pi}{3}\right) m$ થી આપવામાં આવે છે. ગતિ માટે આવર્તકાળ $3.14 \mathrm{~s}$ છે. $t=0$ સમયે કણનો વેગ. . . . . . .$\mathrm{m} / \mathrm{s}$ હશે.View Solution
- 7એક સાદા લોલકનો આવર્તકાળ $1$ મીનીટ છે. જો તેની લંબાઈમાં $44 \%$ નો વધારો કરવામાં આવે તો તેનો નવો આવર્તકાળ કેટલો થશે ?View Solution
- 8$t =0$ થી $t =\tau \;s$ નાં સમયગાળામાં એક સાદા લોલક્નો કંપવિસ્તાર (મૂળ મૂલ્યના $1/e$ જેટલો) છે. $\tau$ એ લોલકનો સરેરાશ જીવનકાળ છે. જ્યારે સાદા લોલકના ગોળામાં (શ્યાનતાને કારણે) વેગના સમપ્રમાણમાં પ્રતિવેગ લાગે છે, જેનો સમપ્રમાણતા અચળાંક $b$ છે, ત્યારે સાદા લોલકનો સરેરાશ જીવનકાળ સેકન્ડમાં કેટલો હશે?(અવમંદન ખુબ જ નાનો છે તેમ માનો)View Solution
- 9પુન: સ્થાપક બળ સ્થાનાંતરના સપ્રમાણમાં અને અવરોધક બળ વેગના સપ્રમાણમાં હોય તેવા કણ પર $Fsin\omega t$ બળ લાગે છે. જો કણનો કંપવિસ્તાર $\omega = {\omega _1}$ માટે મહત્તમ અને કણની ઊર્જા $\omega = {\omega _2}$ માટે મહત્તમ હોય, તો ........ (જ્યાં $\omega_0$ દોલન કરતાં કણની પ્રાકૃતિક આવૃતિ છે)View Solution
- 10View Solutionનીચેનામાંથી કયું સમીકરણ સરળ આવર્તગતિ દર્શાવે છે?
