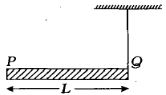
$M $ દળ અને $L$ લંબાઈ ધરાવતા એક સળિયા $PQ$ નો $P$ છેડો જડિત કરેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે, દળ રહિત દોરી વડે બિંદુ $Q$ સાથે બાંધીને આ સળિયાને સમક્ષિતિજ રાખવામાં આવેલ છે. જયારે દોરીને કાપી નાખવામાં આવે, ત્યારે સળિયાનો પ્રારંભિક કોણીય પ્રવેગ કેટલો થશે?

AIPMT 2013, Diffcult
d
When the string is cut, the rod will rotate about \(P.\) Let \(\alpha \) be initial angular acceleration of the rod. Then
When the string is cut, the rod will rotate about \(P.\) Let \(\alpha \) be initial angular acceleration of the rod. Then
Torque, \(\tau = I\alpha = \frac{{M{L^2}}}{3}\alpha \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\)
(Momentum of inertia of the rod about one end = \(\frac{{M{l^2}}}{3}\))
Also, \(\tau = Mg\frac{L}{2}\) \( ...(ii)\)
Equating \((i)\) and \((ii)\), we get
\(Mg\frac{L}{2} = \frac{{M{L^2}}}{3}\alpha \,\,or\,\,\alpha = \frac{{3g}}{{2L}}\)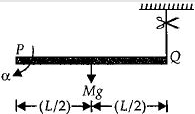
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1અવગણ્ય દ્રવ્યમાન ધરાવતા $1 \;m$ લંબાઈના એક જડ સળિયાના બે છેડા પર અનુક્રમે $5\, kg$ અને $10\, kg$ દ્રવ્યમાનના કણો જોડેલ છે. $5\, kg$ ના કણથી આ તંત્રનું દ્રવ્યમાન કેન્દ્ર આશરે કેટલા અંતરે ($m$ માં) હશે?View Solution
- 2$10\, g$ દળ અને $500\, m/s$ ની ઝડપે એક બુલેટને બારણાંમાં છોડવામાં આવે છે જેથી તે બારણાની વચ્ચે ખૂંચી જાય છે. બારણું $1.0\, m$ પહોળું અને $12\, kg$ વજનવાળું છે. તેનો એક ભાગ જોડેલો છે અને તે તેના શિરોલંબ અક્ષ ને અનુલક્ષીને ઘર્ષણરહિત ભ્રમણ કરે છે. બુલેટ તેમાં ખૂંચે પછી તરત તેની કોણીય ઝડપ કેટલી હશે?View Solution
- 3ચાકગતિ કરતા કણ માટે $a_r = 3\ ms^{-2}, a_T = 4\ ms^{-2}$ છે. જો $a $ અને $a_r$ વચ્ચેનો ખૂણો $\theta$ હોય, તો .......View Solution
- 4$3 \;kg $ દળ અને $ 0.2 \;m$ ત્રિજયાનો એક ઘન ગોળો $7\; m$ ઊંચાઇ એક ઢળતા પાટિયા પરથી ગબડે, તો ચાકગતિઊર્જા ($J$ માં) કેટલી થાય?View Solution
- 5$2.8 \,m / s$ના વેગથી ગોળો ઢાળ પર ઉપર તરફ ગબડે છે,તો તે ઢાળ પર મહત્તમ કેટલા અંતર ($m$ માં ) સુધી ગતિ કરશે?View Solution
- 6સમાન તારમાંથી $P$ અને $Q$ રીંગ બનાવવામાં આવે છે.તેમની ત્રિજયા $r$ અને $nr$ છે. $Q$ ની જડત્વની ચાકમાત્રા $P$ કરતાં $8$ ગણી હોય,તો $n$ કેટલો હશે?View Solution
- 7દળ $m_c$ અને તેનો બાકીનો અડધો ભાગ ચાંદીનો બનેલો છે. તેનું દળ $ m_s $ છે. જો સળિયાની લંબાઈ $ L $ હોય, તો સળિયાના મધ્યબિંદુમાંથી પસાર થતી અને સળિયાને લંબ અક્ષને અનુલક્ષીને સળિયાની જડત્વ ચાકમાત્રા........View Solution
- 8સમાન દળ અને સમાન જાડાઈ ધરાવતી તકતીઓની ઘનતાઓ અનુક્રમે $17 \,g / cm ^3$ અને $51 \,g / cm ^3$ છે. તેમની કેન્દ્રિય અક્ષને અનુલક્ષીને તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર શું થશે?View Solution
- 9$0.9\, kg$ દળ અને $1 \,m$ લંબાઈ ધરાવતા સળિયાના એક છેડાને અનુલક્ષીને ભ્રમણ કરી શકે છે, $0.1\, kg$ દળ અને $80\,m / s$ના વેગથી આવતો કણ નીચેના છેડે ચોંટી જતા કોણીય ઝડપ .......View Solution
- 10એક અક્ષ પર $I$ જડત્વની ચાક્માત્રા ધરાવતું પૈડું $\omega$ કોણીય ઝડપથી ભ્રમણ કરે છે.સ્થિર રહેલું $3I$ જડત્વની ચાકમાત્રા ધરાવતું પૈડું આ અક્ષ પર જોડવામાં આવે તો તંત્રની ગતિઊર્જામાં થતો આંશિક ઘટાડો છે.View Solution
