$(A)$ $\mathrm{E}=\frac{3}{4}\left(\frac{\mathrm{mv}^{2}}{\mathrm{qa}}\right)$
$(B)$ $\mathrm{P}$ બિંદુ આગળ વિદ્યુતક્ષેત્રને કારણે થતાં કાર્યનો દર $\frac{3}{4}\left(\frac{\mathrm{mv}^{3}}{\mathrm{a}}\right)$
$(C)$ $\mathrm{Q}$ બિંદુ આગળ બંને ક્ષેત્રને કારણે થતાં કાર્યનો દર શૂન્ય થાય.
$(D)$ $\mathrm{P}$ અને $\mathrm{Q}$ બિંદુ આગળ મળતા કોણીય વેગમાનના મૂલ્યનો તફાવત $2 mav$ થાય.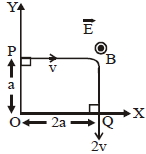
Option \((\mathrm{A})\)
\(\mathrm{W}=\mathrm{k}_{\mathrm{f}}-\mathrm{k}_{\mathrm{i}}\)
\(q E(2 a-0)=\frac{1}{2} m(2 V)^{2}-\frac{1}{2} m V^{2}\)
\(\mathrm{q} \mathrm{E} 2 \mathrm{a}=\frac{3}{2} \mathrm{mV}^{2}\)
\(\mathrm{E}=\frac{3}{4} \frac{\mathrm{mv}^{2}}{\mathrm{qa}}\)
Option \((\mathrm{B})\)
Rate of work done \(\mathrm{P}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{V}}=\mathrm{FV} \cos \theta=\mathrm{FV}\)
Power \(=q \mathrm{EV}\)
Power \(=\mathrm{q}\left(\frac{3}{4} \frac{\mathrm{mV}^{2}}{\mathrm{qa}}\right) \mathrm{V}\)
Power \(=9 \frac{3}{4} \frac{\mathrm{mV}^{3}}{\mathrm{qa}}\)
Power \(=\frac{3}{4} \frac{\mathrm{mV}^{3}}{\mathrm{a}}\)
Option \((\mathrm{C})\)
Angle between electric force and velocity is \(90^{\circ},\) hence rate of work done will be zero at \(\mathrm{Q} .\)
Option (D)
Initial angular momentum \(\mathrm{L}_{\mathrm{i}}=\mathrm{mVa}\)
Final angular momentum \(\mathrm{L}_{\mathrm{f}}=\mathrm{m}(2 \mathrm{V})\) (2a)
Change in angular momentum \(\mathrm{L}_{\mathrm{f}}-\mathrm{L}_{\mathrm{i}}=3 \mathrm{mVa}\)
Download our appand get started for free
Similar Questions
- 1$500$ આંટા ધરાવતી કોઈલલનો વિસ્તાર $50\,cm ^2$ તથા તે $0.14$ છે. અહીં કોણીય વેગ $150\,rad / s$ કોઈલનો અવરોધ $5\; \Omega$ છે,$10\; \Omega$ જેટલાં બાહ્ય અવરોધ સાથે $emf$ પ્રેરીત થાય છે.અવરોધમાંથી વહે તો વિદ્યુતપ્રવાહ........ $A$View Solution
- 2ફ્લૂરેસ્કેન્ટ લેમ્પ ચોકમાં(નાનું ટ્રાન્સ્ફોર્મર) $0.025 \;\mathrm{ms} $ માં પ્રવાહ એકસમાન રીતે $0.25 \;\mathrm{A}$ થી ઘટીને $0\;\mathrm{A}$ થાય છે ત્યારે તે $100 \;\mathrm{V}$ નો રિવર્સ વૉલ્ટેજ ઉત્પન્ન કરે છે.તો ચોકનું આત્મપ્રેરકત્વ($\mathrm{mH}$ માં) કેટલું હશે?View Solution
- 3તારની ચોરસ લૂપ નું સમતલ ચુબકીયક્ષેત્રને લંબ છે. તારનો વ્યાસ $4/mm$ અને $30\,cm$ લંબાઈ નો તાર છે. ચુબકીયક્ષેત્રના ફેરફારનો દર $dB / dt =0.032\, Ts ^{-1} .$ છે તો પ્રેરિત થતો પ્રવાહ $............\times 100\,p\,A$View Solution
તારની અવરોધકતા $1.23 \times 10^{-8}\, \Omega m$ છે.
- 4ગુંચળામાંથી પ્રેરિત થતા $emf$ માટેView Solution
$A$. સમાન ઝડપે ગૂંચળું સમાન ચુંબકીયક્ષેત્રમાં ગતિ કરે છે.
$B$. અસમાન ઝડપે ગૂંયળું સમાન ચુંબકીયક્ષેત્રમાં ગતિ કરે છે.
$C$. સમાન ચુંબકીયક્ષેત્રમાં ગુંચળું ફરે છે.
$D$. સમાન ચુંબકીયક્ષેત્રમાં ગુંચળાનું ક્ષેત્રફળ બદલાય છે.
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 5$10 \;cm$ ત્રિજયા, $500$ આંટા અને $2\;\Omega$ અવરોધ ધરાવતી એક કોઇલને તેનું સમતલ પૃથ્વીના ચુંબકીયક્ષેત્રના સમક્ષિતિજ ધટકને લંબ રહે તેમ મૂકેલ છે. તેને તેના ઊર્ધ્વ વ્યાસ ફરતે $0.25 \;s $ માં $180^o$ ફેરવવામાં આવે છે.આ કોઇલમાં પ્રેરિત થતું $emf $ કેટલું હશે? $(H_E=3.0 \times 10^{-5}\;T )$View Solution
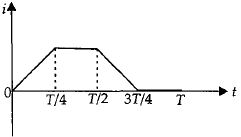
- 6આકૃતિમાં દર્શાવ્યા મુજબ એક ગૂંચળામાં વિદ્યુતપ્રવાહ $i$ એ સમય સાથે બદલાય છે. ગૂંચળામાં સમય સાથે બદલાતા પ્રેરિત $e.m.f.$ માટે કયો આલેખ યોગ્ય છે.View Solution
- 7$0.05\,{m^2}$ અસરકારક ક્ષેત્રફળ અને $800$ આંટા ધરાવતી એક ગુંચળાને $5 \times {10^{ - 5}}\,T$ ચુંબકીય ક્ષેત્ર ને લંબ રાખવામાં આવે છે. જ્યારે આ ગુંચળાના સમતલને તેની કોઈપણ સમસમતલીય અક્ષને અનુલક્ષીને $0.1\; s$ માં $90^{\circ}$ ઘુમાવવામાં આવે, તો આ ગુંચળામાં પ્રેરિત થતું $emf$ કેટલા $V$ હશે?View Solution
- 8$60 \mathrm{~cm}$ લંબાઈનો એક સળિયો $20 \mathrm{rots}^{-1}$ ના નિયમિત કોણીય વેગથી તેના લંબ દ્રીભાજકને અનુલક્ષીને $0.5 T$ ના નિયમિત ચુંબકીય ક્ષેત્રમાં ભ્રમણ કરે છે. ચુંબકીય ક્ષેત્રની દિશા ભ્રમણ અક્ષને સમાંતર છે. સળિયાના બે છેડાઓ વચ્ચે સ્થિતમાનનો તફાવત . . . . . .$\mathrm{V} $છે.View Solution
- 9View Solutionજ્યારે બે ગુચળાને એકબીજાની નજીક રાખવામા આવે ત્યારે તેમની જોડનું અન્યોન્ય પ્રેરકત્વ કોના પર આધાર રાખે?
- 10View Solutionઆદર્શ સ્ટેપ ડાઉન ટ્રાન્સફોર્મરમાં શેનું મૂલ્ય વધે છે?
