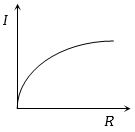
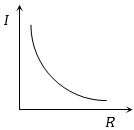
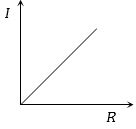
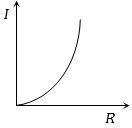
$M$ દળ અને $R$ ત્રિજ્યા ધરાવતા ગોળાની જડત્વની ચાકમાત્રા $I$ છે . જો $M$ ને અચળ રાખવામા આવે તો $I$ વિરુદ્ધ $R$ નો ગ્રાફ નીચેના પૈકી ક્યો હોય $?$
- A
- B
- C
- D
Medium
Download our app for free and get started
d
sphere: \(I=(2 / 5) M R^{2}\) i.e \(I \propto R^{2}\) as \(M\) is constant graph should be parabolic symmetrical about \(I\) axis.
sphere: \(I=(2 / 5) M R^{2}\) i.e \(I \propto R^{2}\) as \(M\) is constant graph should be parabolic symmetrical about \(I\) axis.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
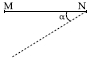
- 1એક પાતળા સળિયા $MN$ ના છેડા $N$ ને સમક્ષિતિજમાં એવી રીતે જોડેલો છે કે જેથી તે શિરોલંબ સમતલમાં મુક્ત રીતે ફરી શકે. જ્યારે સળિયો સમક્ષિતિજ સાથે $\alpha $ નો ખૂણો બનાવે ત્યારે તેને મુક્ત કરવામાં આવે છે તો ત્યારે છેડા $M$ નો વેગ કેટલો હશે?View Solution
- 2$3l$ લંબાઈ ધરાવતા એક દઢ અને દળરહિત સળીયાના બે છેડા આગળ આકૃતિમાં દર્શાવ્યા પ્રમાણે બે દળો લગાડવામાં આવ્યા છે. એક સમક્ષિતિજ અક્ષના $P$ બિંદુ આગળથી કિલકિત કરવામાં આવેલ છે (આકૃતિ જુઓ). જ્યારે તેને પ્રારંભિક સમક્ષિતિજ સ્થિતિમાંથી મુક્ત કરવામાં આવે છે ત્યારે તેનો તાત્ક્ષણિક કોણીય પ્રવેગ ________ થશેView Solution
- 3View Solutionએક કીડી ચાકગતિ કરતી તકતીની કિનારી પર બેઠેલી છે. જો કીડી વ્યાસ પરથી ચાલીને બીજા છેડે પહોંચે ત્યારે તકતીનો કોણીય વેગ કેટલો હશે?
- 4સમાન દ્રવ્યમાન $M$ અને સમાન ત્રિજયા $R$ ધરાવતી ત્રણ વસ્તુઓ $A: $ ( એક ઘન ગોળો ), $B:$ ( એક પાતળી વર્તુળાકાર તકતી ) અને $C: $ ( એક વર્તુળાકાર રીંગ ) છે.તેઓ સમાન કોણીય ઝડપ $\omega \;$સાથે પોતાની સંમિતમાંથી ફરતે ભ્રમણ કરે છે.તેઓને સ્થિર કરવા જરૂરી કાર્યનો જથ્થો $(W) $ કયો સંબંધ સંતોષે છે?View Solution
- 5$D$ વ્યાસ અને $L$ લંબાઈના નળાકારની લંબાઈને લંબ અને તેના ગુરૂત્વકેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 6એક $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીનું એકમ ક્ષેત્રફળ દીઠ દળ $\sigma (r) = kr^2$ મુજબ આપવામાં આવે છે જ્યાં $r$ એ તકતીના કેન્દ્રથી અંતર છે.તો તેના સમતલને લંબ અને દ્રવ્યમાન કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 7$2 \;{kg}$ દળ અને $50 \;{cm}$ ત્રિજ્યાનો ઘન નળાકાર $30^{\circ}$ ખૂણા વાળા ઢાળ પર ઉપર તરફ ગબડીને ગતિ કરે છે. નળાકારના દ્રવ્યમાન કેન્દ્રની ઝડપ $4 \;m/s$ છે. ઢાળવાળી સપાટી પર નળાકારે કેટલું અંતર ($m$ માં) કાપ્યું હશે?View Solution
- 8એક ઘર્ષણવાળા ટેબલ પર $a$ બાજુ અને $m$ દળ ધરાવતો સમઘન પડેલો છે . સમઘનની કોઈ એક સપાટી પર ટેબલની સપાટી થી $3a\over 4 $ ઊંચાઈએ લંબરૂપે $ F$ બળ લગાવવામાં આવે છે. તો $F$ ના કેટલા ન્યૂનતમ મૂલ્ય માટે બ્લોક સરક્યાં વગર નમશે ?View Solution
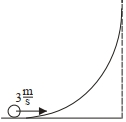
- 9સમાન ધનતાનો એક પોલો ગોળાકાર દડો $3\,m/s$ પ્રારંભિક વેગથી આકૃતિમા દર્શાવ્યા મુજબ વક્ર સપાટી પર ગબડે છે. પ્રારંભિક સ્થાનને અનુલક્ષીને તેણે પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ $........cm$ હશે.$(g=10\,m / s ^2)$ લો.View Solution
- 10એક બળ $\vec{F}=(2 \hat{i}+3 \hat{j}-5 \hat{k}) \,N$ બિંદુ $\vec{r}_1=(2 \hat{i}+4 \hat{j}+7 \hat{k}) \,m$. ઉપર લાગુ કરવામાં આવે છે. તો બિંદુ $\vec{r}_2=(\hat{i}+2 \hat{j}+3 \hat{k}) \,m$ ને અનુલક્ષીને બળ વડે ઉદભવતું ટોર્ક ............ $Nm$ હશે ?View Solution