$M$ દળ અને $R$ ત્રિજયા ધરાવતા નકકર નળાકારને ઢાળ પર મૂકતાં તળિયે તેનો વેગ
Medium
b
Potential energy of the solid cylinder at height \(\mathrm{h}=\mathrm{Mgh}\)
Potential energy of the solid cylinder at height \(\mathrm{h}=\mathrm{Mgh}\)
\(K.E.\) of centre of mass when reached at bottom
\(=\frac{1}{2} M v^{2}+\frac{1}{2} I \omega^{2}=\frac{1}{2} M v^{2}+\frac{1}{2} M k^{2} v^{2} / R^{2}\)
\(=\frac{1}{2} M v^{2}\left(1+\frac{k^{2}}{R^{2}}\right)\)
For a solid cylinder \(\frac{k^{2}}{R^{2}}=\frac{1}{2}\)
\(\therefore \quad \mathrm{K.E.}=\frac{3}{4} M v^{2}\)
\(\therefore \quad M g h=\frac{3}{4} M v^{2}\)
\(v=\sqrt{\frac{4}{3} g h}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$'m'$ દળના એક પદાર્થને જમીન સાથે $45^{\circ}$ ના ખૂણે $'u'$ વેગથી ફેંકવામાં આવે છે. પ્રક્ષિપ્ત બિંદુને અનુલક્ષીને મહત્તમ ઊંચાઈ પર પદાર્થનું કોણીય વેગમાન $\frac{\sqrt{2} \mathrm{mu}^2}{\mathrm{Xg}}$ વડે આપેલ છે તો $'X'$ નું મૂલ્ય ........View Solution
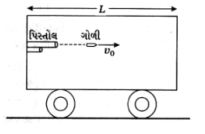
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે $ L $ લંબાઈની એક ટ્રૉલીમાં તેની દીવાલ પર પિસ્તોલ જડેલી છે. (ટ્રૉલી + પિસ્તોલ)નું દળ $M$ છે. આ પિસ્તોલમાંથી $\mathop {{v_0}}\limits^ \to $ વેગથી એક ગોળી છૂટીને સામેની દીવાલ સાથે અથડાય છે, તો આ ગોળી સામેની દીવાલ સાથે અથડાય તે દરમિયાનમાં ટ્રૉલીએ કેટલું અંતર કાપ્યું હશે ?View Solution
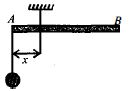
- 3આકૃ તિ માં દર્શાવ્યા મુજબ એક નિયમિત સળિયા $AB$ ને $A$ થી કોઈ ચલિત અંતર $X$ આગળ લટકાવેલો છે. સળિયાને સમક્ષિતિજ ગોઠવવા માટે દળ $m$ ને તેના છેડા $A$ સાથે લટકાવેલ છે. $(m, x)$ ની કિંમતો આપેલ છે. તેનો ગ્રાફ સુરેખા મળે તેના માટે ના ચલ શું હોય શકે?View Solution
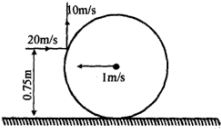
- 4$2\ kg$ પાતળી રિંગની ત્રિજ્યા $0.5\ m$ છે. તે $1\ m/s $ ના વેગથી સમક્ષિતિજ સમતલ પર સરક્યા વિના ગબડે છે. $0.1\ kg$ દળનો નાનો બોલ તેની વિરૂદ્ધ દિશામાં $20\ m/s$ ગના વેગથી ગતિ કરે છે અને રિંગને $ 0.75\ m$ ઉચાઈએ અથડાઈને શિરોલંબ દિશામાં $10\ m/s$ વેગથી ગતિ કરે છે. અથડામણની તરત જ બાદ....View Solution
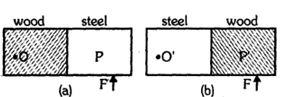
- 5આકૃતિમાં મીટર પટ્ટીનો અડધો ભાગ લાકડાનો અને અડધો સ્ટિલનો બનેલો છે. લાકડાનો ભાગ $O$ પર કિલકિત કરેલો છે. બળ $ F$ સ્ટીલના ભાગે આપવામાં આવે છે. આકૃતિમાં $(b)$ માં સ્ટીલનો ભાગ $ O$ પર કિલકિત કરેલો છે. અને તેટલું જ લાકડાના ભાગ પર આપવામાં આવે છે.View Solution
- 6એક સળિયાની તેના દ્રવ્યમાનકેન્દ્રમાંથી પસાર થતી તેને લંબ એવી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $\frac{1}{{12}}M{L^2}$ છે. હવે સળિયાને મધ્યમાંથી એવી રીતે વાળવામાં આવે છે કે જેથી બનતા બે ભાગ તે જ સમતલમાં નો ખૂણો બનાવે છે. તો આ તંત્રની તે જ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 7View Solutionફલાય વ્હીલને એવી રીતે બનાવવામાં આવે છે જેથી તેનું સંપૂર્ણ દળ તેની રીમ પર સંકેન્દ્રિત થયેલું હોય છે, કારણ કે......
- 8એક બોલને $\alpha=6 t^{2}-2 t$ જ્યાં $t$ સેકન્ડમાં અને $\alpha$ એ $rads ^{-2}$ માં છે, થી ફેરવવામાં આવે છે. $t=0$ એ બોલનો કોણીય વેગ $10 \,rads ^{-1}$ અને કોણીય સ્થાન $4 \,rad$ છે. બોલના કોણીય સ્થાન માટેનું સૌથી યોગ્ય સંબંધ_______હશે.View Solution
- 9બે વર્તૂળાકાર રિંગના દળોનો ગુણોત્તર $1 : 2$ અને વ્યાસોનો ગુણોત્તર $ 2 : 1$ છે. તો તેમની જડત્વની ચાકમાત્રાનો ગુણોત્તર શું હોય?View Solution
- 10એક ચક્ર સ્થિર સ્થિતિમાંથી શરૂ થઈને $20 \,s$ માટે $2 \,rad / s ^2$ નાં નિયમિત દરથી પ્રવેગિત થાય છે. તેને બીજી $10 \,s$ માટે એજ નિયમિત પ્રવેગ સાથે ભ્રમણ કરવાની છુટ આપવામાં આવે છે અને તે અંતે ત્યારબાદની $20 \,s$ સ્થિર થાય છે. ચક્ર દ્વારા કુલ ભ્રમણ થયેલો ખૂણો (રૂડીયનમાં) કેટલો થાય?View Solution
