$M$ દળ અને $R$ ત્રિજ્યાનો એક નક્કર નળાકાર $h$ ઉંચાઈના ઢોળાવવાળા સમતલ પર નીચે ગબડે છે. જ્યારે તે સમતલના તળિયે પહોંચે ત્યારે નળાકારનો કોણીય વેગ શોધો.
Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$R $ ત્રિજ્યા અને $ M $ દળના નિયમિત ગોળાકાર પદાર્થની જડત્વની ચાકમાત્રા $I$ છે. $\theta$ કોણ ધરાવતા ઢાળ પરથી તે રોલિંગ (સરક્યા વિના) કરે છે. ત્યારે તેનો પ્રવેગ કેટલો થાય ?View Solution
- 2એક પૈડું સ્થિર સ્થિતિમાથી $5\ sec$ માં $60\ rad/sec$ ની કોણીય ઝડપ પ્રાપ્ત કરે તો તેણે કાપેલું કોણીય અંતર ....... $rad$ થાય.View Solution
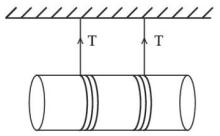
- 3$0.5\,kg$ દળ ધરાવતા એક નળાકાર ને આકૃતિમાં દર્શાવ્યા અનુસાર દળ રહીત બે દોરીઓ વડે લટકાવવામાં આવેલ છે. દોરીઓનો એક સાથે છોડીને નળાકારને તેના પ્રારંભિક સ્થાન થી પતન કરાવવામાં આવે કે જેથી તેની ઝડપ $4\,ms ^{-1}$ મળે, તે અંતર $..............cm$ છે. ( $g =10 ms ^{-2}$ લો. $)$View Solution
- 4જો વર્તુળાકાર માર્ગ પર ગતિ કરતાં કણના સ્થાનાંતર માટે નું સમીકરણ $\theta = 2{t^3} + 0.5$ દ્વારા આપી શકાતું હોય, જ્યાં $\theta $ એ રેડિયનમાં અને $t$ એ સેકંડમાં છે. તો બે સેકંડ પછી કણનો કોણીય વેગ ......... $rad/sec$ હશે.View Solution
- 5$3\; m$ લંબાઈના સળિયાનું એકમ લંબાઈ દીઠ દળ એ તેના એક છેડાથી અંતર $x$ ના સમપ્રમાણમાં બદલાય છે, તો આ સળિયાનું દ્રવ્યમાનકેન્દ્ર તેના એક છેડેથી કેટલા અંતરે ($m$ માં) હશે?View Solution
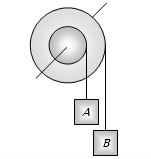
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે બે પૈડાં એક જ અક્ષ પર ફરે છે મોટા પૈડાં ની ત્રિજ્યા નાના પૈડાં ની ત્રિજ્યા કરતાં બમણી છે જો $A$ ને $B$ માટે બાંધેલી દોરી સરકી જતી ના હોય અને $x$ અને $y$ એ $A$ અને $B$ વડે સમાન સમયમાં કાપેલું અંતર હોય તો .....View Solution
- 7$m$ દળનો એક વિસ્ફોટ કણ જમીનથી અમુક ઊચાઈએ આવેલા $ [x - y]$ સમક્ષિતિજ સમતલમાં $x - $ અક્ષ સાથે ગતિ કરે છે. જો તે અચાનક ફૂટીને $ m/4 $ અને $3m/4$ દળ ધરાવતા કણોમાં વહેચાય છે. તે ક્ષણ પછી નાનો કણ $y = 15\ cm$ સ્થાને હોય છે. આ ક્ષણે મોટો કણ $y =$ ........ $cm$ સ્થાન હશે .View Solution
- 8$1\ m$ લંબાઈના હલકાં સળિયાના છેડે $ 5\ kg $ દળના બે ગોળા $ A$ અને $B $ જોડેલા છે. આ દળને બિંદુવત ધારો $A $ માંથી પસાર થતી અને મધ્યબિંદુમાંથી પસાર થતી સળિયાની લંબાઈને લંબ અક્ષો પર જડત્વની ચાકમાત્રાનો ગુણોત્તર ...... થશે.View Solution
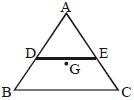
- 9$ABC$ સમબાજુ ત્રિકોણ તકતી છે.$O$ અને $E$ એ $AB$ અને $AC$ના મધ્યબિંદુ છે.$G$ એ કેન્દ્ર છે. $G$ માંથી પસાર થતી અને સમતલ $ABC$ને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા $I _{0}$ છે.જો $ADE$ ભાગને દૂર કરવામાં આવે છે ત્યારે વધેલા ભાગની જડત્વની ચાક્માત્રા તે જ અક્ષને અનુલક્ષીને $\frac{ NI _{0}}{16}$ હોય તો $N=......$View Solution
- 10$2\, kg$ દળના એક કણ માટે, $t$ સમયે તેનું સ્થાન (મીટરમાં) $\overrightarrow r \left( t \right) = 5\hat i - 2{t^2}\hat j$ દ્વારા આપેલ છે. કણનું ઉદગમની સાપેક્ષે $t\, = 2\, s$ સમયે તેનું સ્થાન ($kg\, m^{-2}\, s^{-1}$ માં) શું હશે?View Solution