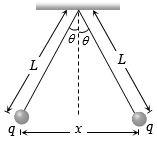
$m$ દળ ધરાવતા અને $q$ વિદ્યુતભાર ધરાવતા બે ગોળાને આકૃતિ મુજબ બાંધેલા છે.જો ખૂણો $\theta$ સૂક્ષ્મ હોય,તો $X$ = _____

Diffcult
a
(a) In equilibrium \(F_e = T sin\theta \) ....... \((i)\)
\(mg = T cos\theta \) ....... \((ii)\)
\(\tan \theta = \frac{{{F_e}}}{{mg}} = \frac{{{q^2}}}{{4\pi {\varepsilon _o}{x^2} \times mg}}\) also \(\tan \theta \approx \sin \theta = \frac{{x/2}}{L}\)
Hence \(\frac{x}{{2L}} = \frac{{{q^2}}}{{4\pi {\varepsilon _o}{x^2} \times mg}}\)
\(==>\) \({x^3} = \frac{{2{q^2}L}}{{4\pi {\varepsilon _o}mg}}\) \(==>\) \(x = {\left( {\frac{{{q^2}L}}{{2\pi {\varepsilon _o}mg}}} \right)^{1/3}}\)
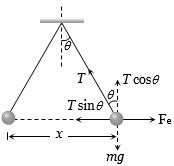
(a) In equilibrium \(F_e = T sin\theta \) ....... \((i)\)
\(mg = T cos\theta \) ....... \((ii)\)
\(\tan \theta = \frac{{{F_e}}}{{mg}} = \frac{{{q^2}}}{{4\pi {\varepsilon _o}{x^2} \times mg}}\) also \(\tan \theta \approx \sin \theta = \frac{{x/2}}{L}\)
Hence \(\frac{x}{{2L}} = \frac{{{q^2}}}{{4\pi {\varepsilon _o}{x^2} \times mg}}\)
\(==>\) \({x^3} = \frac{{2{q^2}L}}{{4\pi {\varepsilon _o}mg}}\) \(==>\) \(x = {\left( {\frac{{{q^2}L}}{{2\pi {\varepsilon _o}mg}}} \right)^{1/3}}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક લાંબા નળાકારીય કદ ધનતા $\rho$ ધરાવતું નિયમિત વિદ્યુતભાર વિતરણ ધરાવે છે. નળાકારીય કદની ત્રિજ્યા $R$ છે. એક $q$ વિદ્યુતભારીત કણ તેની આસપાસ વર્તુળાકાર પથ પર ભ્રમણ કરે છે. વિદ્યુતભારની ગતિઉર્જા ......થશે.View Solution
- 2એક ધન ધાતુના ગોળા પાસે $+ 3Q$ વિદ્યુતભાર છે. જે $-Q$ વિદ્યુતભાર વાળા સુવાહક ગોળીય કવચને સમકેન્દ્રિત છે. ગોળાની ત્રિજ્યા $a$ અને ગોળીય કવચની $b$ છે. $(b > a)$. કેન્દ્રથી $R$ અંતર આગળ $(a < R < b) \,f$ વિદ્યુતક્ષેત્ર ....... છે.View Solution
- 3$1$ કુલંબના બે વિદ્યુતભારોને $1 \,km$ દૂર મૂકવામાં આવે, તો તેમની વચ્ચે લાગતું બળ ............. $N$ હશે.View Solution
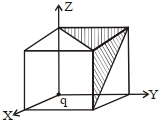
- 4આકૃતિમાં દર્શાવ્યા મુજબ $'q'$ વિજભાર ને સમઘનનાં એક ખૂણા પર ગોઠવવામાં આવ્યો છે. આચ્છાદિત ક્ષેત્રફળમાંથી પસાર થતાં સ્થિત વીજ ક્ષેત્ર $\overrightarrow{ E }$ નું ફ્લક્સ ...... હશે.View Solution
- 5વિદ્યુતભાર $Q$ અને $-3Q$ અમુક અંતરે મૂકેલા છે,$Q$ પર વિદ્યુતક્ષેત્ર $E$ હોય,તો $-3Q$ પર વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 6$h$ ઊંચાઈ અને $R$ બેજની ત્રિજ્યા ધરાવતા શંકુને $\vec E$ વિદ્યુતક્ષેત્રમાં એવી રીતે મૂકવામાં આવે છે કે જેથી વિદ્યુતક્ષેત્ર બેજને સમાંતર રહે.તો શંકુમાં દાખલ થતું વિદ્યુત ફ્લક્સ કેટલું હશે?View Solution
- 7View Solutionવિદ્યુતભારની હાજરીની સાચી કસોટી કઈ છે ?
- 8એક વિદ્યુત ડાયપોલને $4 \times 10^5 \,N / C$ તીવ્રતાના વિદ્યુતક્ષેત્ર સાથે $60^{\circ}$ ના ખૂણો મૂકવામાં આવી છે. તે $8 \sqrt{3} \,Nm$ જેટલુ ટોર્ક અનુભવે છે. જો ડાયપોલની લંબાઈ $4 \,cm$ હોય તો ડાયપોલ પર વિદ્યુતભાર ............... $C$View Solution
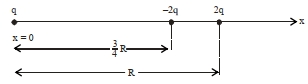
- 9ત્રણ બિંદુવત વીજભારો $q,-2 q$ અને $2 q , x$-અક્ષ પર $x=0, x=\frac{3}{4} R$ અને $x=R$ અંતરે અનુક્રમે ઉદગમથી મૂકેલા આકૃતિમાં દર્શાવેલ છે. જો $q =2 \times 10^{-6}\,C$ અને $R=2\,cm$ હોય તો $-2 q$ વિદ્યુતભારને અનુભવતું પરિણામી બળ ..........$N$ છે.View Solution
- 10ઉગમબિંદુ પર કેન્દ્ર રહે તેમ વિધુતડાઇપોલ $x$-અક્ષ પર મુકેલ છે. $OP$ રેખા $x$-અક્ષ સાથે $\frac{\pi }{3}$ખૂણો બનાવે છે.જો $P$ બિદું આગળ વિધુતક્ષેત્ર $x$-અક્ષ સાથે બનાવેલ ખૂણો $\theta$ હોય તો $\theta$=______View Solution
