$m$ દળ ધરાવતા એક ચોસલાને $k$ સ્પ્રિંગ અચળાંક ધરાવતી એક દળરહિત સ્પ્રિંગ વડે જોડવામાં આવેલ છે. આ ચોસલાને લીસી સમક્ષિતિજ સપાટી પર મુકવામાં આવે છે અને સ્પ્રિંગના બીજા છેડાને આકૃતિમાં બતાવ્યા પ્રમાણે જડવામાં આવેલ છે. જો અચળ બળથી ચોસલાને ખેંચવામાં આવે તો ચોસલા દ્વારા ધારણ કરવામાં આવતી મહત્તમ ઝડ૫ _______ થાય.
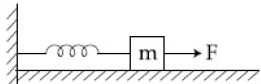

JEE MAIN 2019, Diffcult
d
When \(\,{v_{\max }}\) \(\Rightarrow \) acceleration \(= 0\)
When \(\,{v_{\max }}\) \(\Rightarrow \) acceleration \(= 0\)
\( \Rightarrow \,x = \frac{F}{K}\)
Apply work energy theorem
\(\,{W_{sp}}\) + \(w_f\) = \(\Delta K.E\)
\(\begin{array}{l}
- \frac{1}{2}K{x^2} + F.x = \Delta K.E\,\,\,;\,\, - \frac{1}{2}K\frac{{{F^2}}}{{{K^2}}} + \frac{{{F^2}}}{K}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}mu_{\max }^2\\
\frac{{{F^2}}}{{2K}} = \frac{1}{2}mu_{\max }^{2\,}\,\,\,;\,\,\,\frac{F}{{\sqrt {mK} }} = {V_{\max }}
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $80\; kg$ નો માણસ $6 \;m$ ઉંચી સીડી પર $10$ સેકન્ડ સુધી ચડે છે. તો તે સરેરાશ કેટલા .....$HP$ હોર્સપાવર ઉત્પન્ન કરે ?View Solution
- 2View Solutionવિધાન: બે પદાર્થો વચ્ચેના ઝડપી સંઘાત એ ધીમાં સંઘાત કરતાં વધારે ઉગ્ર હોય છે: જ્યારે પ્રારંભિક અને અંતિમ વેગ સમાન હોય ત્યારે પણ.
કારણ: પ્રથમ કિસ્સામાં વેગમાન વધારે હોય છે.
- 3$8\,kg$ અને $2\,kg$ દળ ધરાવતી બે વસ્તુઓ સમાન ગતિઊર્જા સાથે ગતિ કરે છે. તેઓના વેગમાનોનો ગુણોત્તર $.......$ થશે.View Solution
- 4એક અવકાશયાન કે જેનુ દળ $M$ છે. તે $V$ જેટલા વેગથી ગતિ કરે છે અને અચાનક બે ભાગમાં ફાટે છે. તેનો એક $m$ દળનો ભાગ સ્થિર લઇ જાય છે. ત્યારે બીજા ભાગનો વેગ કેટલો હશે?View Solution
- 5$400\; ms^{-1}$ ના સમક્ષિતિજ વેગથી ગતિ કરતી $10\;g $ દળની એક ગોળી, $2\; kg $ દળના લાકડાના બ્લોક સાથે અથડાય છે, જે $5\; m$ લાંબી ખેંચાઇ ન શકે તેવી દોરીથી લટકાવેલ છે. જેના લીધે બ્લોકનું ગુરુત્વકેન્દ્ર $10\;cm$ શિરોલંબ અંતર વધે છે. બ્લોકની સમક્ષિતિજ દિશામાં બહાર નીકળે ત્યારે ગોળીની ઝડપ (${ms} ^{-1}$ માં) કેટલી હશે?View Solution
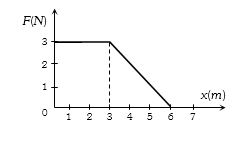
- 6એક પદાર્થ પર લાગતું બળ $F$, તેના સ્થાનાંતર $x$ સાથે આકૃતિમાં દર્શાવ્યા મુજબ બદલાય છે. બળ ન્યુટનમાં અને $x$ મીટરમાં છે. $x=0$ થી $x = 6\; m$ સુધી પદાર્થની ગતિ માટે બળ દ્વારા કેટલું કાર્ય ($J$ માં) થયું હશે?View Solution
- 7$M $ દળનો બ્લોક $ K$ બળ અચળાંક ધરાવતી સ્પિંગ્ર સાથે અથડાવાથી સ્પિંગ્રનું સંકોચન $ L$ થાય છે.તો બ્લોકનું અથડામણ પછીનું મહત્તમ વેગમાન કેટલું થાય?View Solution

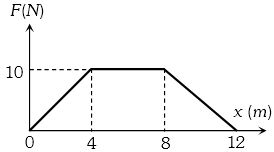
- 8$0.1 kg $ નો પદાર્થનો બળ વિરુધ્ધ સ્થાનાંતરનો આલેખ આપેલ છે.પદાર્થનો શરૂઆતનો વેગ $0 m/s $ હોય,તો $12m $ અંતર કાપ્યા પછી તેનો વેગ કેટલા .............. $m/s$ થાય?View Solution
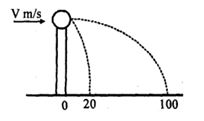
- 9$0.2 kg$ દળનો એક દડો $5m$ ઉંચાઈ પર સ્થિર રહેલો છે. $0.01 kg$ દળની એક ગોળી $V m/s$ ના વેગથી સમક્ષિતિજ દિશામાં ગતિ કરીને દડાના કેન્દ્ર આગળ અથડાય છે. સંઘાત પછી દડો અને ગોળી સ્વતંત્ર રીતે ગતિ કરે છે. થાંભલાના તળિયેથી આ દડો જમીન પર $20 m$ અંતરે અને ગોળી $100 m $ અંતરે અથડાય છે. ગોળીનો પ્રારંભિક વેગ $ V $ કેટલા.......$m/s$ હશે ?View Solution
- 10$2 kg$ નો ટુકડો સમક્ષિતિજ તળિયે $4 m/s$ ની ઝડપે સરકે છે તે અસંકુચિત સ્પ્રિંગ સાથે અથડાય છે. તેનું ગતિક ઘર્ષણબળ $15 N$ અને સ્પ્રિંગ અચળાંક $10, 000 N/m $ છે. તો સ્પ્રિંગ કેટલા......$cm$ સંકોચન પામશે ?View Solution
