($G$ ગુરુત્વાકર્ષણનો અચળાંક ; $\mathrm{M}$પૃથ્વીનું દળ)
Applying energy conservation
Applying energy conservation
\({\mathrm{K}_{1}+\mathrm{U}_{\mathrm{i}}=\mathrm{K}_{\mathrm{f}}+\mathrm{U}_{\mathrm{f}}}\)
\({\frac{1}{2} \mathrm{mu}^{2}+\left(-\frac{\mathrm{GMm}}{\mathrm{R}}\right)=\frac{1}{2} \mathrm{mv}^{2}-\frac{\mathrm{GMm}}{2 \mathrm{R}}}\)
\(\mathrm{v}=\sqrt{\mathrm{u}^{2}-\frac{\mathrm{GM}}{\mathrm{R}}}\)
By momentum conservation, we have
\(\frac{\mathrm{m}}{10} \mathrm{v}_{\mathrm{T}}=\frac{9 \mathrm{m}}{10} \sqrt{\frac{\mathrm{GM}}{2 \mathrm{R}}}\)
and \(\frac{\mathrm{m}}{10} \mathrm{v}_{\mathrm{r}}=\mathrm{mv}\)
\(\Rightarrow \frac{\mathrm{m}}{10} \mathrm{v}_{\mathrm{r}}=\mathrm{m} \sqrt{\mathrm{u}^{2}-\frac{\mathrm{GM}}{\mathrm{R}}}\)
Kinetic energy of rocket
\({=\frac{1}{2} \mathrm{m}\left(\mathrm{v}_{\mathrm{T}}^{2}+\mathrm{v}_{\mathrm{r}}^{2}\right)}\)
\({=\frac{\mathrm{m}}{20}\left(81 \frac{\mathrm{GM}}{2 \mathrm{R}}+100 \mathrm{u}^{2}-100 \frac{\mathrm{GM}}{\mathrm{R}}\right)}\)
\({=\frac{\mathrm{m}}{20}\left(100 \mathrm{u}^{2}-\frac{119 \mathrm{GM}}{2 \mathrm{R}}\right)}\)
\({=5 \mathrm{m}\left(\mathrm{u}^{2}-\frac{119 \mathrm{GM}}{200 \mathrm{R}}\right)}\)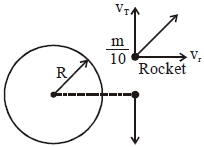
Download our appand get started for free
Similar Questions
- 1View Solutionનીચેનામાથી ક્યો ગુરુત્વસ્થિતિમાન અને પૃથ્વીના કેન્દ્રથી અંતર વચ્ચેનો ગ્રાફ છે
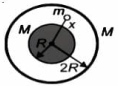
- 2$M$ દળ અને $R$ ત્રિજ્યાનો નિયમિત ગોળો એ એજ દળના પરંતુ $2 R$ ત્રિજ્યાના સમકેન્દ્રીય ગોળાકાર કવચથી આવરિત થયેલો છે. જો બિંદુવત દળ $m$ ને ગોળા દ્વારા આવરીત થયેલા ક્ષેત્રની અંદર આકૃતિમાં દર્શાવ્યા મૂજબ $x(>R)$ અંતરે મૂકેલો છે. તો કણ પરનું પરિણમી ગુરુત્વાકર્ષણ બળ કેટલું છે ?View Solution
- 3જો $M$ દળ ના ગ્રહ ની ફરતે એક $m$ દળનો અને $r$ ત્રિજ્યા ની કક્ષામાં ઉપગ્રહ ફરતો હોય તો તે ઉપગ્રહનો વેગ કેટલો થાય?View Solution
- 4પૃથ્વીની સપાટીથી (પૃથ્વીની ત્રિજ્યા $6.4 \times 10^3 \,km$) $h$ ઊંચાઈ પર એક ઉપગ્રહને રાખવા માટેની જરૂરી ઊર્જા $E_1$ છે અને આ ઉપગ્રહને આ ઊંચાઈ પર વર્તુળાકાર કક્ષામાં રાખવા જરૂરી ગતિ ઊર્જા $E_2$ છે. $E_1$ અને $E_2$ સમાન થાય તેવી ઊંચાઈ $h$ નું મૂલ્ય છેView Solution
- 5બે ગ્રહો $A$ અને $B$ ની ત્રિજ્યાઓ અનુક્રમે $R$ તથા $4 R$ અને તેમની ધનતા અનુક્રમે $\rho$ અને $\rho / 3$ છે. તેઓની સપાટી ઉપર ગુરૂત્વાકર્ષીનું મૂલ્ય $\left(g_A: g_B\right)$ ............. થશે.View Solution
- 6પૃથ્વીની સપાટી પર $g$ નું મૂલ્ય $980 cm/sec^2 $ તો $64\, km$ ઊંચાઈએ $g$ નું મૂલ્ય ........ $cm/{\sec ^2}$ થાય? (પૃથ્વી નીં ત્રિજ્યા $R= 6400 \,km$ )View Solution
- 7$m$ દળનો ઉપગ્રહ પૃથ્વીની સપાટી થી $h$ ઊંચાઈ પર ભ્રમણ કરે છે. જો પૃથ્વીની ત્રિજ્યા $R$ અને ગુરુત્વપ્રવેગ $g$ હોય તો ઉપગ્રહનો વેગ કેટલો થાય ?View Solution
- 8કક્ષામાં જો ઉપગ્રહનો પરિભ્રમણનો સમય $T$ છે તો સ્થિતિઉર્જા એ શેના સમપ્રમાણમાં હશે ?View Solution
- 9View Solutionપૃથ્વીની સપાટી પરથી પ્ર્ક્ષિપ્ત કરેલ રોકેટની નિષ્ક્રમણ ઝડપ......
- 10View Solutionવિધાન : વાતાવરણ વગરની પૃથ્વી ખૂબ જ ઠંડી હોય.
કારણ : વાતાવરણ વગર બધી જ ઉષ્મા છટકી જાય.
