$M$ દળ એ $m$ દળ કરતાં ઘણો વધારે છે. $M$ દળનો ભારે પદાર્થ $v$ વેગથી સ્થિર $m$ દળના હલકા પદાર્થ સાથે સંપૂર્ણ સ્થિતિસ્થાપક સંઘાત અનુભવે છે. તો અથડામણ પછી હલકા પદાર્થનો વેગ કેટલો થશે?
AIIMS 2018, Diffcult
a
From conservation of momentum,
From conservation of momentum,
\(M v+m \times 0=M v_{1}+m v_{2}\)
\(\Rightarrow M\left(v-v_{1}\right)=m v_{2} \ldots\) \((i)\)
Again, from the conservation of kinetic energy (as collision is of elastic nature)
\(\frac{1}{2} M v^{2}+\frac{1}{2} m \times 0=\frac{1}{2} M v_{1}^{2}+\frac{1}{2} m v_{2}^{2}\)
\(\Rightarrow M\left(v^{2}-v_{1}^{2}\right)=m v_{2}^{2} \ldots(\) ii \()\)
On solving equations \((i)\) and \((ii),\) we get
\(\frac{M\left(v-v_{1}\right)}{M\left(v+v_{1}\right)\left(v-v_{1}\right)}=\frac{m v_{2}}{m v_{2}^{2}}\)
\(v_{2}=v+v_{1} \ldots\) \((iii)\)
Now, solving equations \((i)\) and \((iii)\), we get
\(v_{1}=\frac{(M-m) v}{(M+m)}\) and \(v_{2}=\frac{2 M v}{(M+m)}\)
As \(M \gg m\)
\(So , v_{1}=v \Rightarrow v_{2}=v+v=2 v\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$200\, ms^{-1}$ ની ઝડપથી ઉપર તરફ શિરોલંબ દિશામાં ગતિ કરતો પદાર્થ $490\, m$ ઊંચાઈએ બે સમાન ટુકડામાં વિભાજિત થાય છે. એક ટુકડો શિરોલંબ ઉપર તરફ $400\, ms^{-1}$ વેગ થી ગતિ શરૂ કરે છે. તો બીજા ટુકડા થી અલગ થયા પછી થી જમીન સુધી પહોંચવામાં કેટલા ............... $\mathrm{s}$ સમય લેશે?View Solution
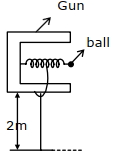
- 2આકૃતિમાં દર્શાવ્યા મુજબ $100\, {N} / {m}$ બળ અચળાંક ધરાવતી સ્પ્રિંગવાળી બંદૂકમાં $100\, {g}$ નો નાનો બોલ $B$ મૂકીને સ્પ્રિંગને $0.05\, {m}$ જેટલી દબાવીને મુક્ત કરવામાં આવે છે. જમીન પર તેનાથી $d$ અંતરે એક બોક્સ મૂકવામાં આવે છે કે જેથી દડો બોક્સમાં પડે. જો બોલ બંદૂકમાંથી જમીનથી $2\, {m}$ ઊંચાઈ સમક્ષિતિજ દિશામાં છોડવામાં આવે છે. તો $d$ નું મૂલ્ય ($m$ માં) કેટલું હશે? $\left(g=10\, {m} / {s}^{2}\right)$View Solution
- 3$l$ લંબાઈની દોરી ધરાવતાં અને $m$ દ્રવ્યમાન ગોલક ધરાવતા એક સાદા લોલને કોઇ એક નાના કોણ $\theta_0$ થી છોડવામાં આવે છે. ખરબચડી સમક્ષિતિજ સપાટી પર મુકેલ $M$ દ્રવ્યમાનના ચોસલાને તે તેના નિમ્ન બિંદુ પર સ્થિતિસ્થાપક રીતે અથડાય છે. તે પાછો ફેંકાય છે અને કોણ $\theta_1$ સુધી પહોંચે છે, તો $M$ દળ કેટલું હશે?View Solution
- 4એક પદાર્થ પર લાગતું બળ $ F(x) = - kx + a{x^3} $ હોય,તો $ x \ge 0 $ માટે પદાર્થની સ્થિતિઊર્જાનો આલેખ નીચે પૈકી કયો થશે?View Solution
- 5View Solutionપદાર્થ પર લાગતું બળ એ તેની ઝડપના વ્યસ્ત પ્રમાણમાં હોય તો પદાર્થની ગતિ ઊર્જા કેવી હશે?
- 6$1.67 \times {10^{ - 27}}kg$ દળ ધરાવતો એક ન્યૂટ્રોન ${10^8}m/s$ વેગથી ગતિ કરીને સ્થિર ડ્યુટેરોન સાથેના સંઘાત બાદ તેની સાથે ચોંટી જાય છે. જો ડ્યુટેરોન નું દળ $3.34 \times {10^{ - 27}}kg$ હોય તો બંનેના સંયોજન નો વેગ કેટલો થાય?View Solution
- 7View Solutionખોટું વિંધાન પસંદ કરો
- 8$l$ લંબાઇની દોરી સાથે એક પદાર્થને બાંધવામાં આવે છે.પદાર્થને કેટલો લઘુત્તમ સમક્ષિતિજ વેગ આપવાથી દોરી સમક્ષિતિજ થાય?View Solution
- 9$M$ દળ અને $v$ વેગ ઝડપે સીધા રસ્તા પર ગતિ કરતાં સાધનનું અટકાયત અંતર ગણો. (( $\mu $ ટાયર અને રસ્તા વચ્ચેનો ઘર્ષણ ગુણાંક છે.)View Solution
- 10$R $ ત્રિજયાની શિરોલંબ લૂપમાં $m$ દ્રવ્યમાનના કોઇ પદાર્થને કેટલા લઘુતમ વેગથી દાખલ કરાવવો જોઇએ કે જેથી તે લૂપમાં સંપૂર્ણ દાખલ થઇ શકે?View Solution
