$R $ ત્રિજયાની શિરોલંબ લૂપમાં $m$ દ્રવ્યમાનના કોઇ પદાર્થને કેટલા લઘુતમ વેગથી દાખલ કરાવવો જોઇએ કે જેથી તે લૂપમાં સંપૂર્ણ દાખલ થઇ શકે?
NEET 2016, Medium
b
Let the tension at point \(A\) be \(T_{A} .\) So, from Newton's second law
Let the tension at point \(A\) be \(T_{A} .\) So, from Newton's second law
\(T_{A}-m g=\frac{m v_{c}^{2}}{R}\)
Energy at point \(A=\frac{1}{2} m v_{0}^{2}\) \(...(i)\)
Energy at point \(C\) is
\(\frac{1}{2} m v_{c}^{2}+m g \times 2 R \ldots .\) \(...(ii)\)
Applying Newton's second law at point \(C\)
\(T_{c}+m g=\frac{m v_{c}^{2}}{R}\)
To complete the loop \(T_{c} \geq 0\)
So, \(m g=\frac{m v_{c}^{2}}{R}\)
\(\Rightarrow \quad v_{c}=\sqrt{g R}\) \(...(ii)\)
From Eqs. \((i)\) and \((ii)\) by conservation of energy
\(\frac{1}{2} m v_{0}^{2}=\frac{1}{2} m v_{c}^{2}+2 m g R\)
\(\Rightarrow \quad \frac{1}{2} m v_{0}^{2}=\frac{1}{2} m g R+2 m g R \quad\left(\because v_{c}=\sqrt{g R}\right)\)
\(\Rightarrow \quad v_{0}^{2}=g R+4 g R\)
\(\Rightarrow \quad v_{0}=\sqrt{5 g R}\)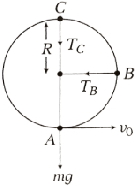
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
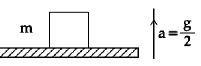
- 1આકૃતિમાં દર્શાવ્યા મુજબ, એક $m$ દળ ધરાવતુ ચોસલું કે જે તેની સ્થિર સ્થિતિમાંથી અચળ પ્રવેગ $g/2$ થી ઊપરની દિશામાં ગતિ શરૂ કરે તેમ રાખેલ છે.$t$ સમયમાં લંબ પ્રત્યાઘાત (normal reaction) દ્વારા કેટલું કાર્ય થશે?View Solution
- 2$32 m $ ઊંચાઇ પરથી દડાને મુકત કરવામાં આવે છે,જો રેસ્ટીટયુશન ગુણાંક $0.5 $ હોય,તો બીજી અથડામણ પછી દડો કેટલા .............. $m$ ઊંચાઈ પ્રાપ્ત કરશે?View Solution
- 3$m $ દળના સાદા લોલક સાથે $m$ દળ અને $v_0$ વેગથી ગતિ કરતો કણ ચોંટી જાય છે.તો ગોળો કેટલી મહત્તમ ઊંચાઇ પ્રાપ્ત કરશે?View Solution
- 4બે સમાન લાદીના ઢેફાઓને બાજુ બાજુએથી બે લાંબી દોરી વડે લટકાવેલા છે. એક બાજુ દોરવામાં આવે છે કે જેથી તેનું ગુરૂત્વકેન્દ્ર $h $ શિરોલંબ અંતર વધે છે. તેને મુક્ત કરવામાં આવે છે અને ત્યારે તે બીજા એક સાથે અસ્થિતિસ્થાપક રીતે સંઘાત પામે છે. તો આ સંયોજનના ગુરૂત્વકેન્દ્રથી વધેલા શિરોલંબ અંતર કેટલું હશે ?View Solution
- 5$m$ દળનો $v$ વેગથી ગતિ કરતો કણ, $2m$ દળવાળા સ્થિર કણ સાથે સંધાત અનુભવે છે. સંધાત બાદ તેઓ એકબીજા સાથે ચોંટી જાય છે અને ગતિ ચાલુ રાખે છે, તો તેમનો વેગ ......... થાય.View Solution
- 6View Solutionબે ગોળાકાર દ્રઢ પદાર્થો વચ્ચે ના અસ્થિતિસ્થાપક સંઘાત માટે ....
- 7રફ સપાટી પર રહેલા $ 10 kg$ દળના બ્લોકનો વેગ $2 m/s $ અચળ રાખવા માટે $5 N $ બળ જરૂરી છે.તો આ બળ દ્વારા $1 $ મિનિટમાં થતું કાર્ય.....$J$View Solution
- 8$m$ દળનો એક પદાર્થ સ્થિર સ્થિતિમાથી $v = a\sqrt s$ મુજબ બદલાતા વેગથી $x-$ અક્ષની દિશામાં ગતિ શરૂ કરે છે. જ્યાં $a$ એ અચળાંક છે અને $s$ એ પદાર્થ દ્વારા કાપેલ અંતર છે. ગતિ શરૂ થયા ના પછીની પ્રથમ એક સેકન્ડમાં પદાર્થ પર તમામ બળો દ્વારા થયેલ કુલ કાર્ય કેટલું હશે?View Solution
- 9$2.5 \,m$ ત્રિજયામાં દોરી સાથે બાંધેલો પદાર્થ અચળ ઝડપથી પરિભ્રમણ કરે છે.દોરીમાં મહત્તમ અને ન્યુનત્તમ તણાવનો ગુણોત્તર $5:3$ હોય ,તો પદાર્થની ઝડપ કેટલી હશે?View Solution
- 10$m$ દળના પદાર્થને $l$ લંબાઇની દોરી વડે લટકાવેલ છે.પદાર્થને સમક્ષિતિજ વેગ આપવાથી દોરી ${60^°}$ નો ખૂણો બનાવે છે.તો સમતોલન સ્થાન પાસે દોરીમાં તણાવ કેટલો હશે?View Solution
