$M$ દળ, $L$ લંબાઈ અને $R$ ત્રિજ્યા ધરાવતા નળાકારના કેન્દ્રમાંથી અને નળાકારની અક્ષને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I = M \left(\frac{ R ^{2}}{4}+\frac{ L ^{2}}{12}\right) $ મુજબ આપવામાં આવે છે. જો આ નળાકારને એક એવા દ્રવ્યમાંથી બનાવવામાં આવે કે જેથી તેના માટે $I$ ન્યૂનતમ રાખવા માટે $\frac LR$ નો ગુણોત્તર કેટલો હોવો જોઈએ?
JEE MAIN 2020, Diffcult
c
\(I=M\left(\frac{R^{2}}{4}+\frac{L^{2}}{12}\right)\)\(...(1)\)
\(I=M\left(\frac{R^{2}}{4}+\frac{L^{2}}{12}\right)\)\(...(1)\)
as mass is constant \(\Rightarrow m =\rho V =\) constant
\(V = constant\)
\(\pi^{2} R l=\) constant \(\Rightarrow R ^{2} L =\) constant
\(2 RL + R ^{2} \frac{ dL }{ dR }=0\)\(...(2)\)
From equation \((1)\)
\(\frac{ dI }{ clR }= M \left(\frac{2 R }{4}+\frac{2 L }{12} \times \frac{ dI }{ dr }\right)=0\)
\(\frac{ R }{2}+\frac{ L }{6} \frac{ dI }{ dR }=0\)
Substituting value of \(\frac{ dI }{ d R }\) from eqution \((2)\)
\(\frac{ R }{2}+\frac{ L }{6}\left(\frac{-2 L }{ R }\right)=0\)
\(\frac{ R }{2}=\frac{ L^{2}}{3 R } \Rightarrow \frac{ L }{ R }=\sqrt{\frac{3}{2}}\)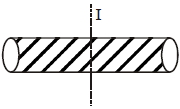
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
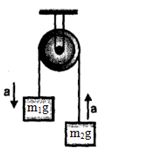
- 1$m_1$ અને $m_2$ દળ ધરાવતા બે પદાર્થને વજન રહિત દોરીના છેડે આકૃતિમાં દર્શાવ્યા મુજબ ગરગડી પરથી લટકાવેલ છે. $m_2 < m_1$ ગરગડી ઘર્ષણ રહિત અને વજન રહિત છે. આ બે પદાર્થથી બનતા તંત્રના દ્રવ્યમાન-કેન્દ્રનો પ્રવેગ.....View Solution
- 2જે પદાર્થનો કોણીય વેગમાન $200\%$ વધારવામાં આવે તો તેની ચાકગતિઊર્જામાં ........ $\%$ વધારો થશે.View Solution
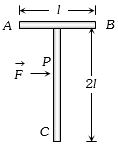
- 3આકૃતિમાં દર્શાવ્યા મુજબ $ T $ આકારનો પદાર્થ લીસી સપાટી પર છે. હવે બિંદુ $ P $ પર,$ AB $ ને સમાંતર દિશામાં બળ $\mathop F\limits^ \to $ એવી રીતે લગાવવામાં આવે છે, જેથી પદાર્થ ચાકગતિ કર્યા વિના ફક્ત રેખીય ગતિ કરે, તો બિંદુ $ C$ ની સાપેક્ષે બિંદુ $P$ નું સ્થાન શોધો.View Solution
- 4$m_1 = fM$ અને $m_2 = (1 -f)\,M\,(f < 1 )$ દળના બે સૂક્ષ્મદળો બાહ્ય અવકાશમાં (બીજી કોઈ વસ્તુની ગુરુત્વઅસરથી દૂર) એકબીજાથી $R$ અંતરે છે. તે બંને તેમના દ્રવ્યમાન કેન્દ્ર ને અનુલક્ષીને વર્તુળાકાર કક્ષા માં $m_1$ એ $\omega _1$ અને $m_2$ એ $\omega _2$ કોણીય વેગથી ગતિ કરે છે.તો આ કિસ્સામાં કોણીય વેગ .....View Solution
- 5View Solutionકોણીય વેગ સદીશ કઈ દિશામાં હોય?
- 6$m$ દળનો એક વિસ્ફોટ કણ જમીનથી અમુક ઊચાઈએ આવેલા $ [x - y]$ સમક્ષિતિજ સમતલમાં $x - $ અક્ષ સાથે ગતિ કરે છે. જો તે અચાનક ફૂટીને $ m/4 $ અને $3m/4$ દળ ધરાવતા કણોમાં વહેચાય છે. તે ક્ષણ પછી નાનો કણ $y = 15\ cm$ સ્થાને હોય છે. આ ક્ષણે મોટો કણ $y =$ ........ $cm$ સ્થાન હશે .View Solution
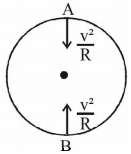
- 7$R$ ત્રિજ્યાનું પૈડું જમીન પર અચળ વેગ $v$ થી ફરે છે. તો પૈડાના સૌથી ટોચ પરના બિંદુનો સંબંધિત પ્રવેગ તેના સૌથી નીચેના બિંદુ ની સાપેક્ષમાં શું હશે ?View Solution
- 8View Solutionજ્યારે દળ, સમતલમાં નિયત બિંદુની ફરતે ચાકગતિ કરતો હોય ત્યારે તેની કોણીય વેગમાનની દિશા ........ હોય.
- 9એક $M$ દળ અને $R$ ત્રિજયાની તકતી તેના કેન્દ્રમાથી પસાર થતી સમક્ષિતિજ અક્ષને અનુલક્ષીને $\omega$ કોણીય વેગથી ફરે છે. હવે જો $m$ દળનો એક ટુકડો તેમાંથી તૂટીને ઉપરની શિરોલંબ દિશામાં ફેકાઈ જાય તો તકતીનો નવો કોણીય વેગ કેટલો થાય ?View Solution
- 10$m$ દળના દ્ઢ પદાર્થના દ્રવ્યમાન કેન્દ્રથી $d$ અંતરે રહેલી અક્ષ પર તે કોણીય વેગ $\omega$ થી ચાકગતિ કરે છે. $G$ માંથી પસાર થતી અક્ષને સમાંતર અક્ષ પર ચક્રાવર્તનની ત્રિજ્યા $K$ છે. પદાર્થની ચાકગતિ ઊર્જા કેટલી થશે ?View Solution
