\(OQ=4\;km\)
\(QR=x\;km\)
The centre of mass will hit the ground at point \(Q\). As the haviour mass comes to rest after bracking
\({x_{cm}} = \frac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}}\)
\(\;Here\;{m_{1\;}} = \frac{{3M}}{4},{m_{2\;}} = \frac{M}{4},\;\)\(\;{x_{1\;}} = OP = 2,\;{x_{2\;}} = OR\; = \;4 + x\)
So,
\(4 = \frac{{\frac{{3M}}{4} \times 2 + \frac{M}{4} \times \left( {4 + x} \right)}}{M}\)
\(4M = \frac{{3M}}{2} + M\left( {1 + \frac{x}{4}} \right)1 + \frac{x}{4} \)\(= \frac{5}{2}\frac{x}{4} = \frac{3}{2}x = 6\;km\)
Hence horizontal range of lighter particle is
\(OR = OQ + QR = 4+6 = 10\; km\)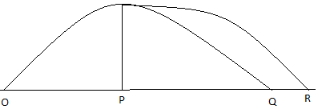
Download our appand get started for free
Similar Questions
- 1View Solutionજો એક પદાર્થ સ્થિર સ્થિતિએ રહેલા તેટલાજ દળના પદાર્થ સાથે અસ્થિતિ સ્થાપક રીતે અથડાય છે સંઘાત પછી તેઓની ઝડપનો ગુણોત્તર શું હશે ?
- 2$ 2.05 \times {10^6}\;kg $ દળ ધરાવતી ટ્રેનનો વેગ $5\; min$ માં $ 5\;m/s $ થી $25\; m/s $ થાય છે,તો એન્જિનનો પાવર કેટલા ......... $MW$ હશે?View Solution
- 3$L $ લંબાઈ અને $M$ દળની એક સમાન શૃંખલા લીસા ટેબલની ધાર પર તેની ચોથા ભાગની લંબાઈ લટકતી રહે તેમ ગોઠવેલી છે. શૃંખલાના લટકતા ભાગને ઉંચકવા માટે જરૂરી કાર્ય શોધો.View Solution
- 4એક એલીવેટર $0.4 m/s $ ની અચળ ઝડપ સાથે $500 kg$ વજનને ઉંચકે છે. તેમાં વપરાયેલ મોટર ઓછામાં ઓછા કેટલા......$H.P.$ હોર્સ પાવરની હશે ?View Solution
- 5સમાન દળ ધરાવતી બે વસ્તુઓ $A$ અને $B$ એક પરિમાણમાં સંપૂણ અસ્થિસ્થાપક અથડામણ (સંધાત) અનુભવે છે. વસ્તુ $A, v_1$ વેગથી ગતિ કરે છે. જ્યારે વસ્તુ $B$ એ સંધાત પહેલા વીરામાવસ્થામાં છે. તંત્રનો સંધાત બાદ વેગ $v_2$ બને છે. $v_1: v_2$ ગુણોતર. . . . . . . થશે.View Solution
- 6$m$દળની ગોળીનો વેગ $v$ છે.તે $M$ દળના બ્લોક સાથે અથડાઇને બ્લોકમાં સ્થિર થાય છે.તો તંત્રની ગતિઊર્જાView Solution
- 7View Solutionજો એક ગોળાને ટોપમાંથી છોડતા હવામાં વિસ્ફોટ કરવામાં આવે તો.....
- 8એક માણસ $5 \,m$ અંતર સુધી એક વજન ઉપાડ છે. મહત્તમ માત્રામાં કાર્ય થાય છે જ્યારે તે...View Solution
- 9આ પ્રશન માં વિધાન $-I$ અને વિધાન $-II$ આપવામાં આવ્યા છે.આ વિધાન પછી આપવામાં આવેલા ચાર વિકલ્પોમાંથી કોઇ એક પસંદ કરો ,કે જે બંને વિધાનોની શ્રેષ્ઠ વ્યાખ્યા આપે છે.View Solution
વિધાન $I:$ $ v$ કણ જેટલી ઝડપથી ગતિ કરતો અને $m$ દળ ધરાવતો એક બિંદુવ્ત કણ, $M$ દળ ધરાવતા અને સ્થિર બીજા બિંદુવ્ત કણ સાથે અથડામણ અનુભવે છે,શકય મહત્તમ ઊર્જા વ્યય $f$ $\left( {\frac{1}{2}m{v^2}} \right)$ સૂત્ર વડે આપી શકાય.જો f $=\left( {\frac{m}{{M + m}}} \right)$
વિધાન $II$ : અથડામણને અંતે જો બંને કણો એકબીજા સાથે જોડાઇ જાય,તો મહત્તમ ઊર્જા વ્યય થશે.
- 10દોરી સાથે બાંધેલ $m$ દળનો પદાર્થ $r$ ત્રિજ્યાના શિરોલંબ વર્તુળમાં ભ્રમણ કરે છે. જો આ પદાર્થનો સૌથી નીચેના બિંદુએ વેગ $\sqrt{7 gr }$ હોય, તો તે નીચેના બિંદુએ ઉદભવતું તણાવ .......... $mg$ હોયView Solution
