$\mathrm{m}$ દળનો પદાર્થ $A$ એક ગ્રહની ફરતે $R$ ત્રિજ્યાની કક્ષામાં ભ્રમણ કરે છે.બીજો $\frac{\mathrm{m}}{2}$ દળ ધરાવતો પદાર્થ $B$ પદાર્થ $A$ સાથે પદાર્થ $A$ના વેગથી અડધા વેગથી અથડાય છે.આ અથડામણ સંપૂર્ણ અસ્થિતિસ્થાપક અથડામણ હોય તો બંને ભેગા પદાર્થ.....
JEE MAIN 2020, Medium
a
Initially, the body of mass \(\mathrm{m}\) is moving in a circular orbit of radius \(\mathrm{R} .\) So it must be moving with orbital speed.
Initially, the body of mass \(\mathrm{m}\) is moving in a circular orbit of radius \(\mathrm{R} .\) So it must be moving with orbital speed.
\(\mathrm{v}_{0}=\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}}\)
After collision, let the combined mass moves with speed \(v_{1 }\)
\({\mathrm{mv}_{0}+\frac{\mathrm{m}}{2} \frac{\mathrm{v}_{0}}{2}=\left(\frac{3 \mathrm{m}}{2}\right) \mathrm{v}_{1}}\)
\({\mathrm{v}_{1}=\frac{5 \mathrm{v}_{0}}{6}}\)
since after collision, the speed is not equal to orbital speed at that point. So motion cannot be circular. since velocity will remain tangential, so it cannot fall vertically towards the planet. Their speed after collision is less than escape speed \(\sqrt{2} v_{0}, \quad\)
so they cannot escape gravitational field. So their motion will be elliptical around the planet.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક માણસની ગતિઊર્જા તેનાથી અડઘું દળ ઘરાવતા છોકરાથી અડઘી છે.જો માણસની ઝડપમાં $ 1 m/s$ નો વઘારો કરવામાં આવે તો બંનેની ગતિઊર્જા સમાન થાય છે. માણસની મૂળ ઝડપView Solution
- 2બે $m$ દળના બ્લોક $A $ અને $B$ ને $L$ લંબાઇ અને $k$ બળઅચળાંક ધરાવતી સ્પિંગ્ર વડે જોડેલાં છે. $m$ દળ ધરાવતો $C$ બ્લોક $v$ વેગથી ગતિ કરીને $A$ સાથે અથડાતા સ્પિંગ્રનું મહત્તમ સંકોચન કેટલું થાય?View Solution
- 3$m$ દળનો પદાર્થ $v$ વેગથી તે જ દિશામાં $ kv$ વેગથી જતાં $nm $ દળના પદાર્થ સાથે અથડાતા,પ્રથમ પદાર્થ સ્થિર થાય,તો બીજા પદાર્થનો વેગView Solution
- 4View Solutionએક સ્પ્રિંગની સ્થિતિ સ્થાપક ઊર્જા......
- 5$m$ દળનો એક ગતિમાન કણ બીજા કોઈ $2m$ દળના સ્થિર કણ સાથે હેડોન સંઘાત અનુભવે છે. તો સંઘાતમાં અથડામણ પામતા કણોમાં કેટલા .............. $\%$ પ્રતિશત ઉર્જા નો ક્ષય થયો હશે?View Solution
- 6$10,000 $ દળની એક ટ્રક $1m$ ઢાળ અને $50 m$ ઉંચાઈ વાળા ઢોળાવના સમતલ પર ચઢાણ કરી રહી છે. જેની ઝડપ $36 km/hr $ છે. એન્જિનનો પાવર.....$kW$ શોધો.($g = 10 m/s^2$)View Solution
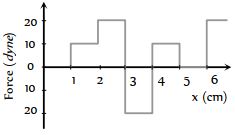
- 7આકૃતિમાં બળ અને સ્થાન વચ્ચેનો સંબંધ બતાવ્યો છે. $x = 1 \;cm$ થી $x = 5 \;cm $ સુધી પદાર્થના સ્થાનાંતર માટે બળ દ્વારા થતું કાર્ય કેટલા ......અર્ગ હશે ?View Solution
- 8લીફ્ટમાં $60\; HP$ ક્ષમતા ધરાવતી ઇલેક્ટ્રિક મોટર મહત્તમ $2000\; \mathrm{kg}$ ઉચકાવી શકે છે. જો લીફ્ટમાં ઘર્ષણબળ $4000 \;\mathrm{N}$ હોય તો મહત્તમ ક્ષમતાથી ભરેલ લિફ્ટ કેટલા ............. $\mathrm{m} / \mathrm{s}$ ના વેગથી ગતિ કરી શકે?View Solution
$\left(1 \;\mathrm{HP}=746 \;\mathrm{W}, \mathrm{g}=10\; \mathrm{ms}^{-2}\right)$
- 9$60$ ફૂટ ઉંચા મકાન પરથી $2 \;kg$ દળના એક બોલને અને $4 kg$ દળના બીજા બોલને એક સાથે ફેંકવામાં આવે છે. બંને બોલ પૃથ્વીની દિશામાં $30$ ફૂટ ઉંચાઈએથી પડ્યા પછી તેમની અનુક્રમે ગતિઊર્જાનો ગુણોત્તર કેટલો હશે ?View Solution
- 10$10 N $ વજનનો બ્લોક $AB$ વક્ર પર સરકે છે. જેને સમક્ષિતિજમાં ખરબચડી સપાટી સાથે જોડેલો છે. ખરબચડી સપાટી અને બ્લોકનો ઘર્ષણાંક $0.20$ છે. જો બ્લોક ટ્રેક પર સમક્ષિતિજથી $1.0 m$ ઉંચાઈએથી સરકીને ખરબચડી સપાટી પર $S$ જેટલા અંતર સુધી ગતિ કરતો હોય તો $S$ ની કિંમત ગણો.......$ m$ [$g = 10 m s^{-2}$]View Solution
