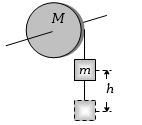
$m$ દળનો પદાર્થ મુકત કરતાં $h$ અંતર કાપ્યા પછી તેનો વેગ

Diffcult
d
Let the acceleration of the mass be \(a\).
Let the acceleration of the mass be \(a\).
Let the angular acceleration of the disc be \(\alpha .\)
since the string moves without slipping on the disc,
\(a=R \alpha\)
\(a=\frac{m g-T}{m}\)
\(T=m g-m a.....(1)\)
\(\alpha=\frac{\tau}{I}\)
where \(\tau=\) torque \(=T R\)
and \(I=\frac{M R^{2}}{2}\)
\(T=\frac{M a}{2}\)
From \((1)\) and \((2)\)
\(a=\frac{2 m g}{m+2 M}\)
\({V}^{2}={u}^{2}+2as\)
\(u=0\)
\(s=h\)
\(V=\sqrt {\dfrac {4mgh}{2m+M}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ચાકમાત્રા ના સિદ્ધાંતો પર કામ કરતાં ભૌતિક ત્રાજવા માં, જ્યારે ડાબા પલ્લાંમાં $5\, mg$ વજન મૂકવામાં આવે છે ત્યારે ત્રાજવાની દાંડી સમક્ષિતિજ થાય છે. બંને ખાલી પલ્લાં સમાન દળ ના છે. તો નીચેનામાથી શું કહી શકાય ?View Solution
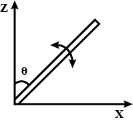
- 2$M$ દળના અને $l$ લંબાઈના એક સ્લેન્ડર એકસમાન સળીયાને એક છેડાથી ધરીમાં એ રીતે જોડેલ છે કે જેથી તે ઊર્ધ્વતલમાં ભ્રમણ કરી શકે (આકૃતિ જુઓ). ધરી પર અવગણ્ય ધર્ષણ છે. મુક્ત છેડાને ઊર્ધ્વ દિશામાં ધરીની ઉપરની તરફ રાખેલ છે અને ત્યારબાદ તેને મુક્ત કરવામાં આવે છે. સળિયાનો કોણીય પ્રવેગ જ્યારે તે ઊર્ધ્વ સાથે $\theta$ ખુણો બનાવે ત્યારે કેટલો હશે?View Solution
- 3દળ $m$ અને લંબાઈ $l$ નો એક તાર વર્તુળાકાર રિંગના સ્વરૂપમાં વાળેલો છે, તો તેની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા શું થશે?View Solution
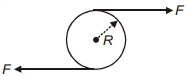
- 4નીયે દર્શાવ્યા પ્રમાણે એક $M$ દળ અને $R$ ત્રિજ્યા વાળી એક નિયમિત તક્તી ઉપર બે સમાન અને વિરુદ્ધ દિશામાંંના બળો સ્પર્શકીય રીતે લગાડવામાં આવે છે. જો તક્તીને તેના કેન્દ્ર પર કિલકીત કરેલી હોય અને તેના સમતલમાં મુક્ત પણે ભ્રમણ કરાવવામાં આવે તો તકતીનો કોણીય પ્રવેગ શું થાય?View Solution
- 5એક પાતળો તાર જેની લંબાઈ $l$ અને દળ $M$ છે તેને વાળીને અડધું વર્તુળ બનાવવામાં આવે છે. તો તારના છેડાઓ પાસેથી પસાર થતી અક્ષ ને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય ?View Solution
- 6View Solutionકણ વર્તૂળાકાર પથ પર ઘટતી ઝડપથી ગતિ કરે છે. સાચું વિધાન નક્કી કરે છે.
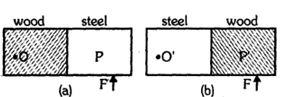
- 7આકૃતિમાં મીટર પટ્ટીનો અડધો ભાગ લાકડાનો અને અડધો સ્ટિલનો બનેલો છે. લાકડાનો ભાગ $O$ પર કિલકિત કરેલો છે. બળ $ F$ સ્ટીલના ભાગે આપવામાં આવે છે. આકૃતિમાં $(b)$ માં સ્ટીલનો ભાગ $ O$ પર કિલકિત કરેલો છે. અને તેટલું જ લાકડાના ભાગ પર આપવામાં આવે છે.View Solution
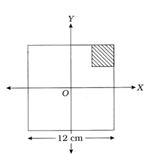
- 8આકૃતિમાં દર્શાવેલ $12\ cm$ લંબાઈની ચોરસ તકતીના એક ખૂણા પરથી $2\ cm $ લંબાઈનો એક ચોરસ કાપી લેવામાં આવે તો બાકી રહેતા ભાગનું દ્રવ્યમાન-કેન્દ્ર, મૂળ ચોરસના કેન્દ્રના સંદર્ભમાં કયાં હશે ? તકતી નિયમિત જાડાઈ અને ઘનતાની છે.View Solution
- 9એક ચકડોળ પોતાની સ્થિર સ્થિતિમાંથી પ્રથમ $5 s$ માં $0.4\ rad s^{-2}$ ના કોણીય પ્રવેગથી ગતિ કરે છે. ત્યારબાદ તે આ અચળ કોણીય પ્રવેગથી $30\ s $ સુધી ચાકગતિ કરે છે અને ત્યારબાદ તે આટલા જ કોણીય પ્રતિપ્રવેગથી સ્થિર થાય છે. ચકડોળ પર ચકડોળના મધ્યબિંદુથી $3\ m$ દૂર બેઠેલા બાળકે આ દરમિયાન કુલ ........ $m$ રેખીય સ્થાનાંતર કર્યું હશે .View Solution
- 10$f_0 = 1.3\, rev/sec$ આવૃતિથી ભ્રમણ કરતી વર્તુળાકાર તકતી $30\, seconds$ માં સ્થિર થાય છે. તો અંદાજિત કોણીય પ્રવેગ ....... $rad/{\sec ^2}$ થશે.View Solution
