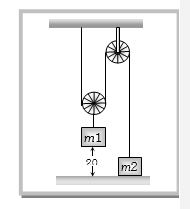
$ m_1 = 4m_2$ છે . $m_2$ ને સ્થિર થવા માટે ........ $cm$ વધારાનું અંતર કાંપવું પડે.
Diffcult
Download our app for free and get started
a
\(v = u + at\) [ \(a = g/2 = \frac{{10}}{2} = 5\,m/{s^2}\)]
\(v = u + at\) [ \(a = g/2 = \frac{{10}}{2} = 5\,m/{s^2}\)]
\(v = 0 + 5 \times 0.4\) \( = 2m/s\,\, = \,200\,cm/sec.\)
\(H = \frac{{{v^2}}}{{2g}} = \frac{{{{\left( {200} \right)}^2}}}{{2 \times 100}}\, = \,20\,cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $Mg$ વજનને એક દોરીનાં મધ્યમાં લટકાવવામાં આવ્યું છે જેના છેડાઓ સમાન સ્તર પર છે. દોરી હવે સમક્ષિતિજ નથી. દોરીને સંપૂર્ણપણે સીધી કરવાં માટે જરરી લઘુત્તમ તણાવ બળ છે.View Solution
- 2સ્થિર પડેલા $0.9 \,kg$ દળના પદાર્થ પર $10\,s$ સુધી અચળ બળ લાગે છે. જો પદાર્થ $250 \,m$ ગતિ કરતો હોય તો તેના પરં લગાવેલ બળનું મૂલ્ય ($N$ માં) કેટલું હશે?View Solution
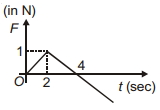
- 3નીચે આપેલ આકૃતિમાં બતાવ્યા પ્રમાણે, પદાર્થ પર લાગતુ બળ એ સમય સાથે બદલાતો રહે છે. જો પદાર્થનુ પ્રારંભિક વેગમાન $\vec{p}$ છે, તો પદાર્થ વડે તેનું $\vec{p}$ વેગમાન ફરીથી જાળવી રાખવા માટે લેવામાં આવતો સમય છેView Solution
- 4$200 \,m / s$ ની ગતિથી ચાલતી $10 \,g$ દળની એક ગોળી લાકડાના પાટિયામાં $5 \,cm$ સુધી ઘૂસીને અટકી જાય છે. ગોળી પર લાગેલો સરેરાશ બળ ................ $N$ હશે.View Solution
- 5$10\, kg$ નો પદાર્થ $10\, m/sec$ ના અચળ વેગથી ગતિ કરે છે.તેના પર $4\, sec$ માટે બળ લાગતા તે $2\, m/sec$ ના વેગથી વિરુધ્ધ દિશામાં ગતિ કરે છે તો પદાર્થ પર ....... $N$ બળ લાગે.View Solution
- 6ગુરૂત્વમુક્ત ઓરડામાં $m_1$ દળનો માણસ ભોંયતળિયાથી $h$ ઉંચાઈએ ઊભો છે. માણસ $m_2$ દળનો બોલ $ u$ જેટલી ઝડપથી અધો દિશામાં ફેંકે છે. જ્યારે બોલ તળિયા પર પહોંચશે ત્યારે માણસનું ભોંય તળિયાથી અંતર શોધો.?View Solution
- 7$20 \,kg$ નો વાંદરો ઊભી દોરડું પકડે છે. જો દોરડા પર $25\,kg$ નું દળ લટકાવવામાં આવે, તો દોરડું તૂટતું નથી, પરંતુ જો તેના પર $25\,kg$ થી વધુ દળ લટકાવવામાં આવે તો તે તૂટી જશે. તે મહત્તમ કેટલા પ્રવેગથી ($m/{s^2}$ માં) વાંદરો દોરડા પર ચઢી શકે? $(g = 10\,m/{s^2})$View Solution
- 8$20\, m/ s$ ની ઝડપથી ગતિ કરતા, $150 \,g$ ના બોલને એક ક્રિકેટર $0.1$ સેકન્ડમાં કેચ કરે છે. તો તેના દ્રારા કેટલું બળ ($N$ માં) અનુભવાશે?View Solution
- 9એક પક્ષી પાંજરા અંદર બેઠેલ હોય,ત્યારે વજન $25 N$ છે.હવે,પક્ષી $2 m/s^2$ ના પ્રવેગથી પાંજરાની અંદર ઉડવાનું શરૂ કરે,ત્યારે નવું વજન ........ $N$ થાય.View Solution
- 10$1 \mathrm{~m}$ લંબાઈનું સાદું લોલક $1 \mathrm{~kg}$ દળનું દોલક ધરાવે છે. તેના પર $10^{-2} \mathrm{~kg}$ દળની બુલેટ $2 \times 10^2 \mathrm{~ms}^{-1}$ ઝડપથી અથડાય છે. આ બુલેટ દોલકની અંદર ખૂંચી જાય છે. દોલકે પાછુ વળે તે પહેલાની ઉંચાઈ_______છે. ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$લો)View Solution