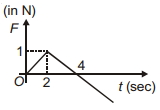
નીચે આપેલ આકૃતિમાં બતાવ્યા પ્રમાણે, પદાર્થ પર લાગતુ બળ એ સમય સાથે બદલાતો રહે છે. જો પદાર્થનુ પ્રારંભિક વેગમાન $\vec{p}$ છે, તો પદાર્થ વડે તેનું $\vec{p}$ વેગમાન ફરીથી જાળવી રાખવા માટે લેવામાં આવતો સમય છે

Diffcult
b
(b)
(b)
\(\tan \theta=\frac{1}{2}=\frac{F_0}{t_0-4}\)
\(\Rightarrow F_0=\frac{t_0-4}{2}\)
Total change in momentum should be zero, then only it will retain its initial momentum.
So, positive area of \(F-t\) curve should be equal to negative area of \(F-t\) curve till time \(t_0\).
\(\frac{1}{2}(4)(1)=\frac{1}{2}\left(t_0-4\right) F_0\)
\(8=\frac{\left(t_0-4\right)}{2} \cdot \frac{\left(t_0-4\right)}{2}\)
\(\left(t_0-4\right)^2=32\)
\(t_0=4+2 \sqrt{2}\)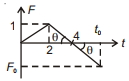
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10 \,kg$ દળને $5 \,m$ લાંબા દોરડાની મદદથી છત પરથી શિરોલંબ રીતે લટકાવવામાં આવેલ છે. દોરડાંના મધ્યબિંદુ આગળ $30 \,N$ જેટલું બળ સમક્ષિતિજ દિશામાં લગાવવામાં આવે છે. દોરડાનો શિરોલંબ સાથેનો કોણ $\theta=\tan ^{-1}\left(x \times 10^{-1}\right)$ છે. $x$ નું મૂલ્ય ........... થશે. $\left(g=10 m / s ^{2}\right)$View Solution
- 2જો બહાર નીકળતા વાયુનો વેગ $300\, m/sec$ ધરાવતા રોકેટ પર લાગતું બળ $210 \,N$ હોય, તો ઇંધણના વપરાશનો દર ($kg/s$ માં) કેટલો હશે?View Solution
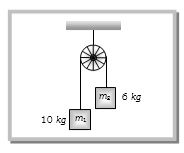
- 3આપેલ તંત્ર માટે તંત્રનો પ્રવેગ ........... $ms^{-2}$ થાય.View Solution
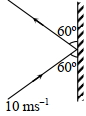
- 4$3\, kg$ દળનો દડો દીવાલ સાથે $60^o$ ના ખૂણે અથડાય છે અને તેટલા જ ખૂણેથી પાછો ફરે છે. સંપર્ક સમય $0.20\,s$ છે. દીવાલ પર લાગતાં બળની ગણતરી કરો.View Solution
- 5હાઇડ્રોજન અણુનું દળ $3.32 \times 10^{-27 } $ $kg$ છે.જો $10^{23}$ હાઇડ્રોજન અણુઓ બીજી પ્રતિ સેકન્ડ, $2$ $cm^2$ ક્ષેત્રફળ ધરાવતી જડિત દિવાલ ઉપર તેના લંબને $45^o $ ના કોણે આપાત થાય છે.અને સ્થિતિસ્થાપક રીતે $10^3$ $ m/s$ ની ઝડપ સાથે પાછા ફરે છે.તો દિવાલ ઉપરનું દબાણ લગભગ ________ થશે.View Solution
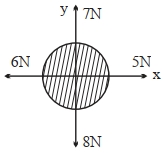
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે $free\,body\,diagram$ $(FBD)$ માટે, ઘણા બધા બળો ' $x$ ' અને ' $y$ ' દિશામાં લગાવવામાં આવે છે. વધારાનો કેટલો અને $x-$અક્ષને કેટલા કોણે બળ લગાડવો પડશે કે જેથી પદાર્થમાં પરિણામી (સમાસ) પ્રવેગ શૂન્ય થાય?View Solution
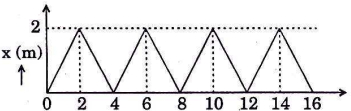
- 7એક-પરિમાણમાં ગતિ કરતાં $0.4$ $ kg$ દળ ધરાવતા પદાર્થ માટે $ x-t $ આલેખ આકૃતિમાં દર્શાવ્યો છે,તો દરેક બળના આઘાતનું મૂલ્ય .......... $N-s$ છે.View Solution
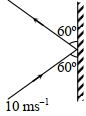
- 8$3\, kg$ દળનો દડો દીવાલ સાથે $60^o$ ના ખૂણે અથડાય છે અને તેટલા જ ખૂણેથી પાછો ફરે છે. સંપર્ક સમય $0.20\,s$ છે. દીવાલ પર લાગતાં બળની ગણતરી કરો.View Solution
- 9$5\, kg$ દળ ધરાવતી વસ્તુને શિરોલંબ ઊધર્વદિશામાં ફેંકવામાં આવે છે. સમગ્ર ગતિ દરમિયાન હવાનો અવરોધ $10 \,N$ નું સતત અપ્રવેગીત બળ ઉત્પન્ન કરે છે. ઉપર ચઢવાની અને નીચે તરફની ગતિ દરમિયાન સમયનો ગુણોત્તર.........થશે.View Solution
- 10એક રોકેટમાં, $2 \,kg/s$ ની દરે ઈધણ (ફયૂલ) બળે છે. આ ઈંધણ રોકેટથી $80 \,km / s$ ના વેગ સાથે બહાર મુક્ત થાય છે. તો રોકેટ પર લગાડેલું બળ ............. $N$ છે.View Solution
