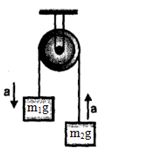
અહી દરેક પદાર્થ નો પ્રવેગ \({\text{a}}\,\, = \,\,\frac{{{{\text{m}}_{\text{1}}}\, - \,\,{m_2}}}{{{m_1}\, + \,\,{m_2}}}\,g\)
દ્રવ્યમાન કેન્દ્ર નો પ્રવેગ ,\(\,\mathop {{{\text{a}}_{{\text{cm}}}}}\limits^ \to \, = \,\,\frac{{{m_1}\,\mathop {{a_1}}\limits^ \to \, + \,\,{m_2}\,\mathop {{a_2}}\limits^ \to }}{{{{\text{m}}_{\text{1}}}\, + \,\,{m_2}}}\)
બંને પદાર્થ વિરુદ્ધ દિશા માં ગતિ કરતાં હોવા થી, \(\mathop {{{\text{a}}_{\text{1}}}}\limits^ \to \,\, = \,\,{\text{ - }}\,\,\mathop {{{\text{a}}_{\text{2}}}}\limits^ \to \,\, = \,\,{\text{a}}\,\)
\(\therefore \,\,{{\text{a}}_{{\text{cm}}}}\, = \,\,\frac{{{m_1}a\,\, - \,\,{m_2}a}}{{{m_1}\, + \,\,{m_2}}}\,\,\,\, = \,\,a\,\left( {\frac{{{m_1}\, - \,\,{m_2}}}{{{m_1}\,\, + \,\,{m_2}}}} \right)\,\)
\( = \,\,\left( {\frac{{{m_1}\, - \,\,{m_2}}}{{{m_1}\, + \,\,{m_2}}}} \right)\,\,\, \cdot \,g\,\,\,\left( {\frac{{{m_1}\, - \,\,{m_2}}}{{{m_1}\, + \,\,{m_2}}}} \right) = \,\,{\left( {\frac{{{m_1}\, - \,\,{m_2}}}{{{m_1}\, + \,\,{m_2}}}} \right)^2}\,g\)
Download our appand get started for free
Similar Questions
- 1View Solutionફલાય વ્હીલને એવી રીતે બનાવવામાં આવે છે જેથી તેનું સંપૂર્ણ દળ તેની રીમ પર સંકેન્દ્રિત થયેલું હોય છે, કારણ કે......
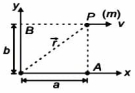
- 2એક કણ $x$ -અક્ષને સમાંતર સીધી રેખામાં અયળ વેગથી ગતિ કરી રહ્યો છે. સદિશ સ્વરૂપમાં ઊગમ બિંદુને અનુલક્ષીને કોણીય વેગમાન શોધો.View Solution
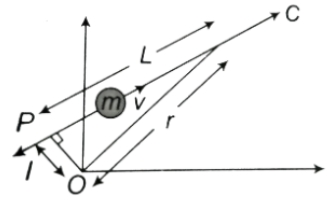
- 3$m$ દળ $v$ વેગથી $PC$ દિશામાં ગતિ કરે છે.તો તેનું કોણીય વેગમાન $O$ ને અનુલક્ષીને કેટલું થાય?View Solution
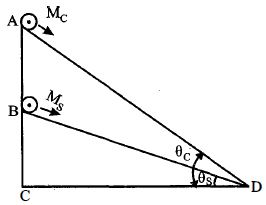
- 4આકૃતિમાં $M_c$ દળનું નળાકાર અને $M_s$ દળના ગોળાને અનુક્રમે બે ઢોળાવના બિંદુઓ $A$ અને $B$ પર મૂકેલા છે. જો તેઓ ઢોળાવ પર સરક્યાં વગર સમાન પ્રવેગથી ગતિ કરતાં હોય તો $\frac{{\sin \,{\theta _c}}}{{\sin \,{\theta _s}}}$ નો ગુણોત્તર કેટલો થાય?View Solution
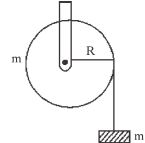
- 5$m $ દળ ધરાવતા પદાર્થને વજનરહિત દોરી વડે $m$ દળ અને $R$ ત્રિજયા ધરાવતા સમાંગી પોલા નળાકાર પર લટકાવવામાં આવે છે.જો દોરી નળાકાર પર સરકે નહિ તો તે સ્થિતિમાં આપેલ પદાર્થ કેટલા ગુરુત્વપ્રવેગથી નીચે પડશે?View Solution
- 6$2\, kg$ દળનો કોઈ કણ લીસ્સા સમક્ષિતિજ ટેબલ પર છે અને તે $0.6\, m$ ત્રિજ્યાના વર્તુળાકાર માર્ગ પર ગતિ કરે છે. જમીનથી ટેબલની ઊંચાઈ $0.8\, m$ છે. જો કણની કોણીય ઝડપ $12\, rad\, s^{-1}$ હોય તો વર્તુળના કેન્દ્રની એકદમ નીચે જમીન પર કોઈ બિંદુ ને અનુલક્ષીને તેના કોણીય વેગમાનની કિંમત ....... $kg\, m^2\,s^{-1}$ થાય.View Solution
- 7લીસા સમક્ષિતિજ ટ્રેક પર $v$ ઝડપે ગતિ કરતી એ લાંબી ટ્રોલીનાં એક છેડે એક બાળક ઊભો રહેલો છે, જો, બાળકએ ટ્રોલીનાં બીજા છેડાં તરફ $u$ ઝડપે દોડવાનું શરૂ કરે છે તો તંત્ર (ટ્રોલી+બાળક) નું દ્રવ્યમાન કેન્દ્ર કેટલી ઝડપે ગતિ કરશે ?View Solution
- 8$m$ દળનો એક કણ એ વેગ $v$ થી સમક્ષિતિજ સાથે $30^{\circ}$ નો ખૂણો બનાવીને પ્રક્ષિપ્ત ગતિ કરે છે. આ કણ જ્યારે મહત્તમ ઉંચાઈ પ્રાપ્ત કરે તે સમયે, ગતિની શરૂઆતના બિંદુની સાપેક્ષે કણના કોણીય વેગમાનનું મૂલ્ય ફેટલું હશે?View Solution
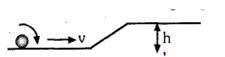
- 9ઘનગોળો ઘર્ષણ રહિત સપાટી પર રોલિંગ કરે છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે સ્થાનાંતરીત વેગ $v\ \ m/s$ થી ગતિ કરીને ઢોળાવ વાળા સમતલ પર ચઢે છે. ત્યારે $v$ કેટલું હોવું જોઈએ ?View Solution
- 10એક ઘન ગોળો ગબડતી ગતિમાં છે.ગબડતિ ગતિ (લોટણ ગતિ) માં પદાર્થ સ્થાનાંતરીત ગતિઊર્જા $(K_t) $ અને ભ્રમણીય ગતિઊર્જા $(K_r)$ એક સાથે ધરાવે છે.આ ગોળા માટે $ K_t: (K_t+ K_r)$ નો ગુણોત્તર છે.View Solution
