Angular momentum, \(\overrightarrow{ L }=\overrightarrow{ r } \times m \overrightarrow{ v }\)
\(\Rightarrow|\overrightarrow{ L }|= rmv \sin \theta\)
At maximum point, velocity is \(v = v \cos \theta= v \cos (30)=\frac{\sqrt{3} v }{2}\) only (direction: towards horizontal) and no vertical velocity is present.
The maximum height reached will be
\(h=\frac{v^{2} \sin ^{2} \theta}{2 g}\)
\(\Rightarrow h =\frac{ v ^{2} \sin ^{2}\left(30^{\circ}\right)}{2 g }\)
\(\Rightarrow h =\frac{ v ^{2}}{8 g }\)
\(L = rmv \sin \theta\)
\(\Rightarrow L = mvh\)
\(\Rightarrow L = m \times \frac{\sqrt{3} v }{2} \times \frac{ v ^{2}}{8 g }\)
\(\Rightarrow L =\frac{\sqrt{3} mv ^{3}}{16 g }\)
Download our appand get started for free
Similar Questions
- 1સમાન દ્રવ્યમાન $M$ અને સમાન ત્રિજયા $R$ ધરાવતી ત્રણ વસ્તુઓ $A: $ ( એક ઘન ગોળો ), $B:$ ( એક પાતળી વર્તુળાકાર તકતી ) અને $C: $ ( એક વર્તુળાકાર રીંગ ) છે.તેઓ સમાન કોણીય ઝડપ $\omega \;$સાથે પોતાની સંમિતમાંથી ફરતે ભ્રમણ કરે છે.તેઓને સ્થિર કરવા જરૂરી કાર્યનો જથ્થો $(W) $ કયો સંબંધ સંતોષે છે?View Solution
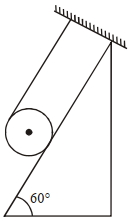
- 2$m$ દળના ઘન નળાકાર પર દોરી વિટાળીને ઢાળ પર આકૃતિ મુજબ છે,જો સ્થિત ઘર્ષણાંક $0.4$ હોય તો ઘન નળાકાર અને ઢાળ વચ્ચે લાગતું ઘર્ષણબળ કેટલું હશે?View Solution
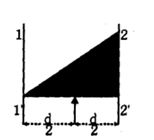
- 3View Solutionઆકૃતિમાં કઇ અક્ષ પર કોણીય પ્રવેગ વધુ થશે અને બળ ત્રિકોણ ફ્રેમના મધ્યબિંદુ પર લાગે છે.
- 4અડધી રિંગની તેની અક્ષને આધારે સમતલને અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
- 5જો એક તકતીની તેની અક્ષ ને આધારે જડત્વની ચાકમાત્રા $I$ હોય તો તેના તેજ સમતલમાં રહેલા સ્પર્શક ના આધારે તેની જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
- 6સમક્ષિતિ સપાટી પર ગબડતી $50 \mathrm{~kg}$ દળની એક તકતીના દ્રવ્યમાનકેન્દ્રનો વેગ $0.4 m/s$ છે તો આ તકતી ને અટકાવવા માટે કરવું પડતું કાર્ય ........... $J$View Solution
- 7નીચે બે વિધાનો આપેલા છે : એક વિધાન $A$ અને બીજું કારણ $R$ વડે દર્શાવેલ છે.View Solution
વિધાન $A :$ $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી વર્તુળાકાર તકતી લગભગ $X, Y$ અક્ષ (તેના પ્લેનમાંથી પસાર થતી) અને $Z-$ અક્ષ જે તેના પ્લેન પર લંબ છે તેને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે $I_{x}, I_{y}$ અને ${I}_{z}$ છે. ત્રણેય અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા સમાન હશે.
Reason $R$ : ચાકગતિ કરતાં દઢ પદાર્થનું દળ અને આકાર નિશ્ચિત હોય છે.
ઉપર આપેલા વિધાનો માટે નીચેનામાંથી યોગ્ય વિકલ્પ પસંદ કરો.
- 8$1\,kg$ દળની વસ્તુનો સ્થાન સદિશ $\overrightarrow{ r }=(3 \hat{ i }-\hat{ j }) \,m$ અને તેનો વેગ $\overrightarrow{ v }=(3 \hat{ j }+\hat{ k }) \,ms ^{-1}$ છે. કોણીય વેગમાનનું મૂલ્ય $\sqrt{x} \,Nm$ મળે છે તો $x$ નું મૂલ્ય ............ હશે.View Solution
- 9સમાન ચક્રાવર્તન ત્રિજ્યા ધરાવતી એક રિંગ અને ઘન ગોળો તેના કેન્દ્રોમાંથી પસાર થતી અક્ષની અનુલક્ષીને ભ્રમણ કરે છે. પરિભ્રમણની અક્ષ રિંગના સમતલને લંબરૂપ છે. રિંગની ત્રિજ્યા અને ગોળાની ત્રિજ્યાનો ગુણોત્તર $\sqrt{\frac{2}{x}}$ છે. $x$ ની કિંમત ...... છેView Solution
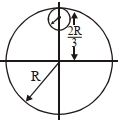
- 10આકૃતિમાં દર્શાવ્યા અનુસાર $R$ ત્રિજયા અને $9$ $M$ દળ ધરાવતી સમાન વર્તુળાકાર તકતીમાંથી નાની $\frac{R}{3}$ ત્રિજયાની સમકેન્દ્રિય તકતી દૂર કરવામાં આવેલ છે. તકતીના સમતલને લંબ અને તકતીના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષી બાકી રહેલ તકતીની જડત્વની ચાકમાત્રા ___View Solution