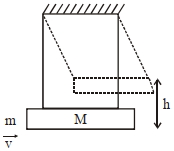
$M=5.99 \,kg$ દળ ધરાવતું એક મોટું ચોસલું બે દળરહિત દોરીઓ વડે લટકાવવામાં આવેલ છે. $m=10\, g$ દળ ધરાવતી ગોળીને ચોસલાંમાં ફાયર (ફોડવામાં) કરવામાં આવે છે અને તે તેમાં ઘૂસી જાય છે. (ચોસલું$+$ગોળી) પછી ઉપર તરફ ગતિ કરે છે, આ દોલક (ચોસલું$+$ગોળી) તેમની માપના અંત્ય બિંદુ આગળ ક્ષણભાર સ્થિર થાય તે પહેલા તેમના દ્રવ્યમાન કેન્દ્ર શિરોલંબ દિશામાં $h=9.8\, cm$ ઊંચાઈએ પહોંચે છે. સંધાત પહેલા તરત જ ગોળીની ઝડપ ..... હશો. ($g =9.8\, ms ^{-2}$ લો.) ($m/s$ માં)

JEE MAIN 2021, Diffcult
c
From energy conservation,
From energy conservation,
\([\) after bullet gets embedded till the system comes momentarily at rest \(]\)
\(( M + m ) g h =\frac{1}{2}( M + m ) v _{1}^{2}\)
\(\left[ v _{1}\right.\) is velocity after collision]
\(\therefore v _{1}=\sqrt{2 gh }\)
Applying momentum conservation, (just before and just after collision)
\(mv =( M + m ) v _{1}\)
\(v =\left(\frac{ M + m }{ m }\right) v _{1}=\frac{6}{10 \times 10^{-3}} \times \sqrt{2 \times 9.8 \times 9.8 \times 10^{-2}}\)
\(\approx 831.55\, m / s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m$ દળનો પદાર્થ $v$ વેગથી $2m$ દળના સ્થિર પદાર્થ સાથે અથડાય છે. $m$ દળ કેટલી ગતિઊર્જા ગુમાવશે?View Solution
- 2$m$ દળ ધરાવતા પથ્થરને, દોરી વડે બાંધી, નિયમિત ઝડપ સાથે શિરોલંબ વર્તુળમાં ફેરવવામાં આવે છે. દોરીમાં તણાવ...View Solution
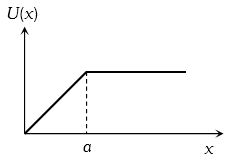
- 3View Solutionપદાર્થની સ્થિતિઊર્જાનો આલેખ આપેલ છે,તો બળનો આલેખ કયો થશે?
- 4એક પાણીના પંપની પાવર $4 \,kW$ છે. જો $g=10 \,ms ^{-2}$, તો તે $1$ મિનીટ માં. $20 \,m$ ઊંચાઈ પર પાણીનાં જથ્થોને માત્રા ને .............. લીટર લઈ જઈ શકેView Solution
- 5પાણીના પંપનો પાવર $2\;kW$ છે. જો $g = 10\,m/{\sec ^2}$ હોય, તો $1 \;min$ માં કેટલું પાણી ($liter$ માં) $10\; m$ ઊંચાઇ સુધી લઈ જઈ શકાય?View Solution
- 6$k$ બળ અચળાંક ધરાવતી સ્પ્રિંગની લંબાઇ $ x = 0 $ થી $ x = {x_1} $ વધારતાં કેટલું કાર્ય થશે?View Solution
- 7$100\,kW$ ટ્રાન્સમીટર દ્વારા એક કલાક્માં આદર્શ સ્થિતિમાં વિખેરીત થતી ઊર્જા$......$હશે.View Solution
- 8એક નાનો કણ તેની પ્રારંભિક સ્થિતિ $2 \hat{i}+3 \hat{j}-4 \hat{k}$ થી $5 \hat{i}-2 \hat{j}+\hat{k}$ પર $5 \hat{i}+2 \hat{j}+7 \hat{k} \;N$ બળની અસર હેઠળ ગતિ કરે છે. થતાં કાર્યનું મૂલ્ય ($J$ માં) કેટલું હશે?View Solution
- 9પાણીનો પંપ $A$ આડછેદવાળી નળીમાં $ \rho $ ઘનતા ધરાવતું પ્રવાહી $v$ વેગથી ગતિ કરાવે છે.તો પંપનો પાવર કેટલો થાય?View Solution
- 10વેગમાન $P$ અને દળ $m$ ધરાવતી કાર રફ રોડ પર ગતિ કરે છે.જો ટાયર અને રોડ વચ્ચેનો ઘર્ષણાંક $m$ હોય,તો સ્ટોપિંગ ડીસ્ટન્સ કેટલું થશે?View Solution
