મીટરબ્રીજની બે ભુજાઓના અવરોધો અનુક્રમે $5\,\Omega$ અને $R\,\Omega$ છે. જયારે અવરોધ $R $ ની સાથે સમાન અવરોધનો શંટ જોડતાં નવો બેલેન્સ પોઇન્ટ $1.6 l_1 $ મળે છે. અવરોધ $R=$ .................. $\Omega$
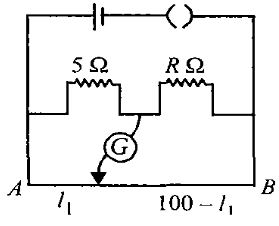

AIPMT 2014, Diffcult
b
At balance point
At balance point
\(\frac{5}{R}=\frac{l_{1}}{100-l_{1}}\) \(\ldots(i)\)
In the second case,
Substituting this value in eqn. \((i)\), we get
\({\frac{5}{R}=\frac{25}{75}} \)
\({R=\frac{375}{25}\, \Omega=15\, \Omega}\)
At balance point
\(\frac{5}{(R / 2)}=\frac{1.6 l_{1}}{100-1.6 l_{1}}\) ....\((ii)\)
Divide eqn. \((i)\) by eqn. \((ii),\) we get
\({\frac{1}{2}=\frac{100-1.6 l_{1}}{1.6\left(100-l_{1}\right)}}\)
\({160-1.6 l_{1}=200-3.2 l_{1}} \)
\({1.6 l_{1}=40 \quad \text { or } \quad l_{1}=\frac{40}{1.6}=25\, \mathrm{cm}}\)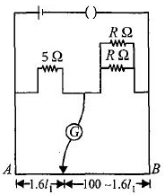
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
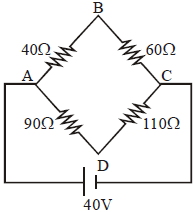
- 1પરિપથમાં $40\ \Omega, 60\ \Omega, 90\ \Omega$ અને $110\ \Omega$ જોડેલા છે. $AC$ વચ્ચે $40\, V$ ની બેટરી જોડેલ છે તો $BD$ વચ્ચે વૉલ્ટેજ ......... $V$View Solution
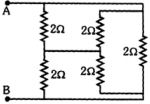
- 2$AB$ ના છેડા વચ્ચેનો સમતુલ્ય અવરોધ............. $\Omega$ છે.View Solution
- 3એક તારનો અવરોધ $R$ છે જો તેને ખેંચીને તેની લંબાઈ બમણી કરવામાં આવે તો નવો અવરોધ કેટલો થાય?View Solution
- 4બે સમાન $emf$ ધરાવતા પરંતુ જુદો જુદો $r_{1}$ અને $r_{2}$ આંતરિક અવરોધ ધરાવતા બે કોષોને અવરોધ $R$ સાથે શ્રેણીમાં જોડવામાં આવેલાં છે. જેનાં માટે બીજા કોષને સમાંતર સ્થિતિમાનનો તફાવત શૂન્ય થાય તે અવરોધ $R$ નું મૂલ્ચ .......થશે.View Solution
- 5કોપરની પટ્ટી અને જર્મેનિયમની પટ્ટીને રૂમ તાપમાનથી $80\, K$ તાપમાન સુધી ઠંડી પાડવામાં આવે તો તેમના અવરોધ વિષે શું કહી શકાય?View Solution
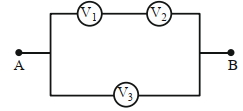
- 6આકૃતિમાં દર્શાવ્યા મુજબ પરસ્પર ભિન્ન આંતરિક અવરોધ ધરાવતા ત્રણ વોલ્ટમીટરોને જોડવામાં આવ્યા છે. જ્યાંરે $A$ અને $B $ની વચ્ચે અમુક સ્થિતિમાનનો તફાવત લગાવવામાં આવે છે ત્યારે $V_1, V_2$ અને $V_3$ અવલોકનો મળે છે. સાચો વિકલ્પ પસંદ કરો.View Solution
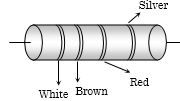
- 7આપેલ તારના અવરોધનું મૂલ્ય કેટલા ............... $k \Omega$ થાય?View Solution
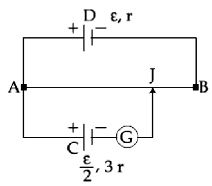
- 8$L$ લંબાઇનો અને $12\, r$ નો અવરોધ ધરાવતા એક પોટેન્શીયોમીટર તાર $AB$ અને $\varepsilon$ જેટલું $emf$ અને $r$ જેટલો આંતરિક અવરોધ ધરાવતા કોષ $D$ સાથે જોડવામાં આવે છે. $\varepsilon/2$ જેટલું $emf$ અને $3r$ જેટલો આતંરિક અવરોધ ધરાવતા કોષ $C$ ને આકૃતિમાં દર્શાવ્યા મુજબ જોડવામાં આવે છે. ગેલ્વેનોમીટરમાં દર્શાવતું શૂન્ય આવર્તન માટેની લંબાઈ $AJ$ _______ હશે.View Solution
- 9View Solutionવાહકનો વિશિષ્ટ અવરોધ કોની સાથે વધે?
- 10શ્રેણીમા જોડેલા બે અવરોધોનો સમતુલ્ય અવરોધ $s$ છે.જયારે તેમને સમાંતર જોડવામાં આવે,તો સમતુલ્ય અવરોધ $p$ મળે છે.જો $s=np$ હોય,તો $n$ નું લઘુત્તમ મૂલ્ય કેટલું હોવું જોઈએ?View Solution
