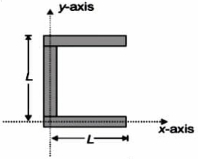
નીચે આકૃતિ દશાવેલ પરિસ્થિતિનું દ્રવ્યમાન કેન્દ્ર નકકી કરો. ત્રણેય સળિયાઓના દળ અને લંબાઈ સમાન છે

Medium
c
(c)
(c)
Here, the coordinates of the centre of mass of the three rods are:
\(\left(0, \frac{ L }{2}\right),\left(\frac{ L }{2}, 0\right),\left(\frac{ L }{2}, L \right)\)
The arrangement is symmetric about the line \(y=\frac{L}{2}\)
Hence the y coordinate of the centre of mass is \(\frac{L}{2}\).
Now,\(x\) coordinate of the centre of mass \(=\frac{\sum m_i x_i}{\sum m_i}\)
\(=\frac{ L }{3}\)
Therefore , the centre of mass of the arrangement is at \(\left(\frac{ L }{3}, \frac{ L }{2}\right)\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
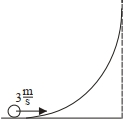
- 1સમાન ધનતાનો એક પોલો ગોળાકાર દડો $3\,m/s$ પ્રારંભિક વેગથી આકૃતિમા દર્શાવ્યા મુજબ વક્ર સપાટી પર ગબડે છે. પ્રારંભિક સ્થાનને અનુલક્ષીને તેણે પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ $........cm$ હશે.$(g=10\,m / s ^2)$ લો.View Solution
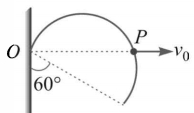
- 2એક પાતળી પણ દઢ અર્ધવતુળ વાયરની ફેમ જેની ત્રિજ્યા $r$ છે તેને $O$ આગળ લટકાવેલ છે અને તે પોતાના જ લંબગત સમતલ પર ફરે છે. એક હળવા $Peg$ $P$ ને $O$ થી શરૂ કરી અચળ વેગ $v _0$ થી આડી દિશામાં ગતિ કરે છે, અને ફ્રેમને ઊંચે લઈ જવાય છે. જ્યારે તે લંબ જોડે $60^{\circ}$ નો ખૂણો બનાવે ત્યારે આ ફ્રેમનો કોણીય વેગ શોધો.View Solution
- 3View Solutionકણ નિયમિત વર્તુળમય ગતિ કરે છે. કયાં બિંદુની સાપેક્ષે તેનું કોણીય વેગમાન અચળ રહે છે.
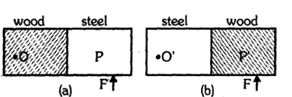
- 4આકૃતિમાં મીટર પટ્ટીનો અડધો ભાગ લાકડાનો અને અડધો સ્ટિલનો બનેલો છે. લાકડાનો ભાગ $O$ પર કિલકિત કરેલો છે. બળ $ F$ સ્ટીલના ભાગે આપવામાં આવે છે. આકૃતિમાં $(b)$ માં સ્ટીલનો ભાગ $ O$ પર કિલકિત કરેલો છે. અને તેટલું જ લાકડાના ભાગ પર આપવામાં આવે છે.View Solution
- 5ચાકગતિ કરતા બે પદાર્થનું કોણીય વેગમાન સમાન છે પરંતુ તેમની જડત્વની ચાકમાત્રા અનુક્રમે $I_1$ અને $I_2$ છે. ($I_1$ > $I_2$) કયા પદાર્થની ગતિ ઊર્જા વધુ હશે ?View Solution
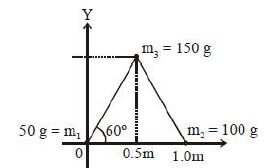
- 6આકૃતિમાં દર્શાવ્યા મુજબ $50\, g$, $100\, g$ અને $150\, g$ દળ ધરાવતા ત્રણ કણને $1\, m$ લંબાઈ ધરાવતા સમબાજુ ત્રિકોણ પર મૂકેલા છે તો દ્રવ્યમાન કેન્દ્રના $(x, y)$ યામ શું થશે?View Solution
- 7ઘન ગોળાની ભૌમિતિક અક્ષ પર જડત્વની ચાકમાત્રા $ I$ છે. જો તેને પીગાળીને $r$ ત્રિજ્યા અને $ t $ જાડાઈની તકતી બનાવવામાં આવે છે. જો તેને સ્પર્શક અક્ષ (જે તકતીના સમતલને લંબ) પર જડત્વની ચાકમાત્રા $ I$ જેટલી જ છે. ત્યારે $ r$ ની કિંમત ....... થાય.View Solution
- 8$M$ દળ, $L$ લંબાઈ અને $R$ ત્રિજ્યા ધરાવતા નળાકારના કેન્દ્રમાંથી અને નળાકારની અક્ષને લંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $I = M \left(\frac{ R ^{2}}{4}+\frac{ L ^{2}}{12}\right) $ મુજબ આપવામાં આવે છે. જો આ નળાકારને એક એવા દ્રવ્યમાંથી બનાવવામાં આવે કે જેથી તેના માટે $I$ ન્યૂનતમ રાખવા માટે $\frac LR$ નો ગુણોત્તર કેટલો હોવો જોઈએ?View Solution
- 9એક લીસો ગોળો $A$ ઘર્ષણરહીત સમક્ષીતિજ સપાટી પર કોણીય વેગ $\omega$ તથા દ્રવ્યમાન કેન્દ્રના વેગ સાથે ગતિ કરે છે. તે બીજા સમાન ગોળા $B$ સાથે સ્થીતિસ્થાપક સંઘાત અનુભવે છે. દરેક જગ્યાએ ઘર્ષણ અવગણતા સંઘાત બાદ તેમની કોણીય ઝડપ $\omega_A$ અને $\omega_B$ હોય તો......View Solution
- 10એક વર્તુળાકાર રિંગ $30^o$ ખૂણાવાળા ઢાળ પરથી સરક્યાં વગર ગબડે છે. તો તેનો તે ઢાળ પર રેખીય પ્રવેગ કેટલો હશે?View Solution
