નીચે આપેલ માહિતી પરથી $OH^-$ આયનની સર્જન-ઉષ્માની કીમત $252\,^oC$ તાપમાને.....$KJ$ શોધો.
${H_2}{O_{(l)}} \to \,\,H_{(aq)}^ + + \,\,OH_{(aq)}^ - \,;\,\,\,\Delta H\,\, = \,\,57.32\,\,KJ\,;$
${H_2}_{(g)} + \,\,\frac{1}{2}\,\,{O_2}_{(g)} \to \,\,{H_2}{O_{(1)}}\,;\,\,\Delta H\,\, = \,\, - 286.20\,\,KJ$
Diffcult
Download our app for free and get started
b
\({H_{2(g)}} + \,\,\frac{1}{2}\,\,{O_2}\,\, \to \,\,{H_2}\,{O_{({l})}}\,;\,\,\Delta H\,\, = \,\, - 288.20\,\,KJ\)
\({H_{2(g)}} + \,\,\frac{1}{2}\,\,{O_2}\,\, \to \,\,{H_2}\,{O_{({l})}}\,;\,\,\Delta H\,\, = \,\, - 288.20\,\,KJ\)
\(\Delta {H_r} = {\mkern 1mu} {\mkern 1mu} \Delta {H_{f({H_2}O,{\kern 1pt} {\kern 1pt} {l})}} - {\mkern 1mu} {\mkern 1mu} \Delta {\mkern 1mu} {H_{f({H_2}O,{\kern 1pt} {\kern 1pt} g)}} - \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \Delta {H_{f{\kern 1pt} ({O_2},{\kern 1pt} g)}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \)
\({\mkern 1mu} \therefore {\mkern 1mu} {\mkern 1mu} \, - 286.20{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \Delta {H_{f({H_2}O{\kern 1pt} ({l}))}}\)
\(So,\,\,\Delta {H_{f({H_2}O\,,\,\,{l})}} = \,\, - 286.\,\,20\)
\({H_2}{O_{({l})}}\, \to \,\,H_{(aq)}^ + \, + \,\,OH_{(aq)}^ - \,\,;\,\,\,\Delta H\,\, = \,\,57.32\,\,KJ\)
\(\Delta {H_r} = \,\,\Delta H_{f({H^ + },\,\,aq)}^ \circ \,\, + \,\,\Delta H_{f(O{H^ - },\,\,aq)}^ \circ - \,\,\Delta H_{f({H_2}O\,,\,{l})}^ \circ \)
\(57.32\,\, = \,\,0\,\, + \,\,\Delta H_{f(O{H^ - },\,\,aq)}^ \circ - ( - 286.20)\)
\(\Delta H_{f(O{H^ - },\,\,aq)}^ \circ = \,\,57.32\,\, - \,286.20\,\, = \,\, - 228.88\,\,KJ\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$300\, K$ એ એક મોલ આદર્શ વાયુને $10 \,dm^3$ થી $20$ $dm^3$ ના કદમાંથી પ્રતિવર્તીં સમઉષ્મીય પ્રસરણ માટે $\Delta H$ ......$KJ$ થશે.View Solution
- 2$MgCO_3$ $_{(s)}$ $\rightarrow$$MgO$$_{(s)} +$ $CO_2$$_{(g)}$ પ્રક્રિયા માટે $\Delta$$S =$ ......View Solution
- 3$NH_4Cl$$_{(s)}$ $\rightarrow$ $NH_3$$_{(g)}$ + $HCl$$_{(g)}$ આ પ્રક્રિયા દરમિયાન એન્ટ્રોપી ...... છે.View Solution
- 4View Solutionસમતાપી પ્રકમ માટે નીચેનામાંથી શું સાચું છે ?
- 5નીચેના પ્રકમો પરથી પ્રકિયા $B + D \rightarrow E + 2C$ માટે $\Delta H$ નું મૂલ્ય કેટલા ........... $\mathrm{kJ/mol}$ હશે તે જણાવો.View Solution
$\Delta H \,(kJ/mol)$ $\frac 12 A \rightarrow B$ $+150$ $3B \rightarrow 2C + D$ $-125$ $E + A \rightarrow 2D$ $+350$ - 6એન્ટ્રોપી $(S)$ ને થર્મોડાયનેમિક્સ માપદંડ ગણતા આપમેળે થતા દરેક પ્રક્રમ માટે સ્વયંભૂયિતાની શરત ........View Solution
- 7$27\,^oC$ એ $10 $ મોલ ઓક્સિજન વાયુ ધરાવતા $5$ લીટર સીલીન્ડર છે. કારણ કે તે છિદ્ર નથી તુરંત જ લીક થાય છે. બધો જ વાયુ વાતાવરણમાં બહાર ફેલાય છે. અને સીલીન્ડર ખાલી થાય છે. જો વાતાવરણ દબાણ $1.0$ વાતાવરણ હોય તો વાયુ દ્વારા થતું કાર્ય કેટલું થશે ?View Solution
- 8$X \,gm$ ઈથેનાલ $(CH_3CHO)$ ને બોમ્બ કેલેરીમીટરમાં સળગાવે છે અને $Y$ જુલ ઉષ્મા ઉત્પન્ન થાય છે. તો .....View Solution
- 9અચળ કદે પ્રણાલી પર$ 500$ જુલ ઉષ્મા પસાર કરવામાં આવે તો પરિણામે પ્રણાલીનું તાપમાન વધીને $20^oC$ થી $25^oC$ થાય છે. તો પ્રણાલીની આંતરિક ઊર્જામાં થતો ફેરફાર ......$J$View Solution
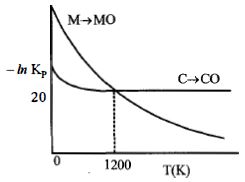
- 10નીચેનો આલેખ એ પ્રક્રિયાઓ $M(s) + \frac{1}{2}{O_2}(s)\, \to \,MO(s)\,$ અને $C(s) + \frac{1}{2}{O_2}(g)\, \to \,CO(s)\,$ માટે $- In\,K_p$ વિરુદ્ધ તાપમાનનો ફેરફાર દર્શાવે છે. તો સાયુ વિધાને ઓળખો.View Solution
