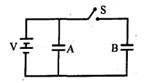
Energy in each capacitor is \(\frac{1}{2} cV ^2\)
when switch is opened
\(Q\) on \(2^{nd}\) capacitor is \(cv\) even after introduction of dielectric \(Q\) remain same but
\(C\) will become \(KC\)
Energy \(=\frac{ Q ^2}{2 C ^2}=\frac{( cv )^2}{2\left( K _{ l }\right)}=\frac{ cv ^2}{2 k }\)
Energy is set is \(\frac{1}{2} cv ^2\)
same as before
after dielectric insertion
\(c\) become \(kc\)
Energy \(=\frac{1}{2}( kc ) v ^2\)
\(=\frac{ kcv ^2}{2}\)
Total energy initially \(=\frac{1}{2} c v^2+\frac{1}{2} c v^2=c^2 \cdots(1)\)
Total energy after opening switch \(= k \frac{ cv ^2}{2}+\frac{ cv ^2}{2 k }\)
\(=\frac{c v^2}{2}\left( k +\frac{1}{ k }\right)\)
put \(k=3\)
\(=\frac{ cV ^2(10)}{2 \times 3}=\frac{5 CV ^2}{3} \ldots(2)\)
\((1)\) \(\div(2)\)
\(=3 / 5\)
Download our appand get started for free
Similar Questions
- 1$1\ \mu F$ કેપેસીટન્સ ધરાવતું બુંદ $8$ સમાન ત્રિજ્યા ધરાવતા બુંદમાં વિભાજીત થાય છે તો દરેક નાના બુંદનું કેપેસીટન્સ....$\mu F$View Solution
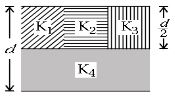
- 2એક સમાંતર પ્લેટ કેપેસિટરની પ્લેટનું ક્ષેત્રફળ $A,$ તેનું કેપેસિટન્સ $C$ અને પ્લેટો વચ્ચેનું અંતર $d$ છે.જેમાં $K_1,K_2,K_3$ અને $K_4$ ડાઇઇલેકિટ્રક અચળાંકવાળા ચાર ડાઇઇલેકિટ્રકોના આકૃતિમાં દર્શાવ્યા પ્રમાણે ભરેલાં છે.જો કોઇ એક જ ડાઇઇલેકિટ્રક પદાર્થને વાપરતાં તેટલું જ કેપેસિટન્સ $ C$ મળે,તો ડાઇઇલેકિટ્રક અચળાંક $ K=$ ________View Solution
- 3View Solutionજવલનશીલ પ્રવાહી લઈ જતા વાહનમાં સામાન્ય રીતે જમીનને અડકે તેવી ધાતુની સાંકળ રાખવામાં આવે છે.
- 4$10\;cm$ ત્રિજયા ધરાવતા પોલા ગોળાને એવી રીતે વિદ્યુતભારિત કરવામાં આવે છે કે જેથી તેની સપાટી પરનું સ્થિતિમાન $80\;V$ થાય. ગોળાના કેન્દ્ર પર સ્થિતિમાન કેટલું હશે?View Solution
- 5બે પ્લેટો વડે સમાંતર પ્લેટ કેપેસિટર રચેલ છે. દરેક પ્લેટનું ક્ષેત્રફળ $100\ cm^2, \,1\ mm$ અંતરે અલગ કરેલી છે. એક $5.0$ ડાઈ ઈલેકટ્રીક અચળાંંક ધરાવતા ડાઈ ઈલેકટ્રીક અને ડાઈ ઈલેકટ્રીક સ્ટ્રેન્થ $1.9 \times 10^7\ V/m$ પ્લેટોની વચ્ચે ભરવામાં આવે છે. ડાઈ ઈલેકટ્રીક બ્રેક ડાઉન કર્યા સિવાય કેપેસિટર પર સંગ્રહ કરી શકાતો મહત્તમ વિદ્યુતભાર શોધો.View Solution
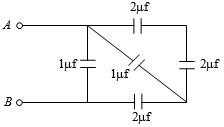
- 6આપેલ તંત્રમાં $A$ અને $B$ વચ્ચે સમતુલ્ય કેપેસિટન્સ કેટલા .....$\mu\ f$ થશે?View Solution
- 7બે કેપેસિટરો $C_1$ અને $C_2$ ને અનુક્રમે $120\ V$ અને $200\ V$ ચાર્જ કરેલ છે. તે જાણવામાં આવ્યું છે કે બંનેને એકબીજાને જોડતાં દરેક એક પરનો સ્થિતિમાન શૂન્ય બનાવી શકાય તેથી.....View Solution
- 8વિધાન $-1$ : સમસ્થિતિમાન પૃષ્ઠ પર વિજભારને એક સ્થાનથી બીજા સ્થાને લઈ જવા માટે કોઈ કાર્ય કરવું પડતું નથી.View Solution
વિધાન $-2$ : સમસ્થિતિમાન પૃષ્ઠ પર વિદ્યુતબળની રેખાઓ સપાટીને લંબ હોય છે.
- 9$1\,\mu F$ કેપેસીટન્સ ધરાવતા સમાંતર પ્લેટ કેપેસીટર ની એક પ્લેટ $+2\,\mu C$ વિજભારે અને બીજી પ્લેટ $+4\,\mu C$ વિજભારે હોય તો તે બે પ્લેટ વચ્ચે કેટલા ......$V$ વિદ્યુતસ્થિમાનનો તફાવત ઉત્પન્ન થશે?View Solution
- 10એક સમાંતર પ્લેટ કેપેસિટર પાસે $20\, kV$ સ્થિતિમાન અને $2 \times 10^{-4} \,\mu F$ કેપેસિટન્સ છે. જો પ્લેટનું ક્ષેત્રફળ $0.01\, m^2$ હોય અને પ્લેટો વચ્ચેનું અંતર $2\ mm$ હોય તો માધ્યમનું ડાઈઈલેકટ્રીક અચળાંક શોધો.View Solution
