નીચે બે વિધાનો આપેલા છે : એક વિધાન $A$ અને બીજું કારણ $R$ વડે દર્શાવેલ છે.
વિધાન $A :$ $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી વર્તુળાકાર તકતી લગભગ $X, Y$ અક્ષ (તેના પ્લેનમાંથી પસાર થતી) અને $Z-$ અક્ષ જે તેના પ્લેન પર લંબ છે તેને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે $I_{x}, I_{y}$ અને ${I}_{z}$ છે. ત્રણેય અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા સમાન હશે.
Reason $R$ : ચાકગતિ કરતાં દઢ પદાર્થનું દળ અને આકાર નિશ્ચિત હોય છે.
ઉપર આપેલા વિધાનો માટે નીચેનામાંથી યોગ્ય વિકલ્પ પસંદ કરો.
JEE MAIN 2021, Medium
Download our app for free and get started
b
\(I_{z}=I_{x}+I_{y}\) (using perpendicular axls theorem)
\(I_{z}=I_{x}+I_{y}\) (using perpendicular axls theorem)
\(l = mk ^{2}\) (K: radius of gyratlon)
so \(m K_{z}^{2}=m K_{x}^{2}+m K_{y}^{2}\)
\(K_{z}^{2}=K_{x}^{2}+K_{y}^{2}\)
so radius of gyration about axes \(x, y\) and \(z\) won't be same hense asseration \(A\) is not correct reason \(R\) is correct statement (property of a rlgid body)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક કણએ $(0,8)$ બિંદુુથી શરૂ થાય છે અને $\vec{v}=3 \hat{i} \,m / s$ ના નિયમિત વેગ સાથે ગતિ કરે છે. તો $5 \,s$ પછી ઊગમબિંદુ અનુલક્ષીને કણનો કોણીય વેગમાન .......... $kg m ^2 / s$ હશે. (કણ નું દળ $1 \,kg$ છે)View Solution
- 2બે વર્તૂળાકાર રિંગના દળ અને ત્રિજ્યાઓના ગુણોત્તર અનુક્રમે $1 : 2$ અને $ 2 : 1$ છે. તો જડત્વની ચાકમાત્રાનો ગુણોત્તર કેટલો થશે ?View Solution
- 3View Solutionઘન ગોળો,ઘન નળાકાર,તકતી અને રીંગ ઢાળ પર મૂકતાં તળિયે એકસાથે કોણ આવશે?
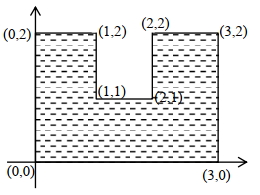
- 4આક્રુતિમાં દર્શાવ્યા અનુસાર $10 \mathrm{~kg}$ દળ ધરાવતી અને દર્શાવેલ પરિમાણ ધરાવતી એક નિયમીત પાતળી ધાત્વીય પ્લેટ (તક્તિ) દર્શાવેલ છે. જો તક્તિના દ્રવ્યમાન કેન્દ્રની $x$ યામ અને $\mathrm{y}$ ની ગુણોત્તર $\frac{n}{9}$ છે.$n$ નું મૂલ્ય. . . . . .થશે.View Solution
- 5$2$ $m$ ત્રિજ્યાની એક ગરગડી $ F = (20t -5t^2)$ ન્યૂટનનાં લગાડેલા સ્પર્શીંય બળથી (જ્યાં $t$ સેક્ન્ડમાં મપાય છે.) તેની અક્ષ આસપાસ ઘુમાવવા (ફેરવવા) માં આવે છે. જો ગરગડીની તેને ભ્રમણાક્ષ આસપાસ જડત્વની ચાકમાત્રા $10\; kg\ m^2$ હોય તો, ગરગડી તેની પોતાની ગતિની દિશા ઉલ્ટાવે તે પહેલા તેને કરેલા ભ્રમણોની સંખ્યા કેટલી હશે?View Solution
- 6View Solutionઢોળાવવાળા સમતલ પરથી ઘન ગોળા સ્થિર સ્થિતિમાંથી ગબડી નીચે આવે છે તેજ સમયે લંબચોરસ બ્લોક પણ સ્થિર સ્થિતિમાંથી તેજ સમતલ પરથી સરકીને નીચે આવે છે ત્યારે.......
- 7$70\, kg$ નો એક માણસ બેઠેલી સ્થિતિમાથી હવામાં ઊભી છલાંગ લગાવે છે. કૂદકો મારીને પોતાને ઊંચકવા માટે તે માટે માણસ જમીનને અચળ બળ $F$ થી ધકેલે છે. તે કૂદકો મારે તે પહેલા દ્રવ્યમાન કેન્દ્ર $0.5\, m$ જેટલું ઊંચકાય છે. કૂદકો માર્યા પછી દ્રવ્યમાન કેન્દ્ર વધુ $1\, m$ ઉપર જાય છે. તો સ્નાયુઓ દ્વારા આપવામાં આવેલ પાવર કેટલો હશે? ( $g\, = 10\, ms^{-2}$)View Solution
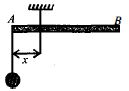
- 8આકૃ તિ માં દર્શાવ્યા મુજબ એક નિયમિત સળિયા $AB$ ને $A$ થી કોઈ ચલિત અંતર $X$ આગળ લટકાવેલો છે. સળિયાને સમક્ષિતિજ ગોઠવવા માટે દળ $m$ ને તેના છેડા $A$ સાથે લટકાવેલ છે. $(m, x)$ ની કિંમતો આપેલ છે. તેનો ગ્રાફ સુરેખા મળે તેના માટે ના ચલ શું હોય શકે?View Solution
- 9$10\, g$ દળ અને $500\, m/s$ ની ઝડપે એક બુલેટને બારણાંમાં છોડવામાં આવે છે જેથી તે બારણાની વચ્ચે ખૂંચી જાય છે. બારણું $1.0\, m$ પહોળું અને $12\, kg$ વજનવાળું છે. તેનો એક ભાગ જોડેલો છે અને તે તેના શિરોલંબ અક્ષ ને અનુલક્ષીને ઘર્ષણરહિત ભ્રમણ કરે છે. બુલેટ તેમાં ખૂંચે પછી તરત તેની કોણીય ઝડપ કેટલી હશે?View Solution
- 10સમાન દળ ' $M$ અને ' $2 R$ ' જેટલી ત્રિજ્યા ધરાવતા ચાર વસ્તુઆની ઝડત્વની ચાકમાત્રા $(M.I.)$ નીચે મુજબ છેView Solution
$I _{1}=$ તેના વ્યાસને અનુલક્ષીને ધન ગોળાની $M.I.$
$I _{2}=$ તેની અક્ષને અનુલક્ષીને ધન નળાકારની $M.I.$
$I _{3}=$ તેના વ્યાસને અનુલક્ષીને ધન તક્તિની $M.I.$
$I _{4}=$ તેના વ્યાસને અનુલક્ષીને પાતળી વર્તુળાકાર રીંગની $M.I.$
જો $2\left( I _{2}+ I _{3}\right)+ I _{4}=x \cdot I _{1}$ હોય તો $x$ નું મૂલ્ય ........થશે.