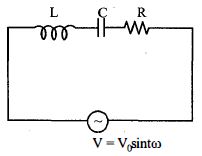
નીચે એક $LCR$ પરિપથ આપેલ છે. હવે એક નવા $C '$ કેપેસીટરને $C$ કેપેસીટર સાથે જોડવામાં આવે છે જેના કારણે પરિપથનો પાવર ફેક્ટર એક મળે છે. તો આ નવો કેપેસીટર $C'$ને પરિપથ સાથે કેવી રીતે જોડેલો હશે?

JEE MAIN 2015, Diffcult
c
Power factor
Power factor
\(\cos \phi=\frac{R}{\sqrt{R^{2}+\left[\omega L-\frac{1}{\omega\left(C+C^{\prime}\right)}\right]^{2}}}=1\)
On solving we get,
\(\omega L=\frac{1}{\omega\left(C+C^{\prime}\right)}\)
\(C' = \frac{{1 - {\omega ^2}LC}}{{{\omega ^2}L}}\)
Hence option \((c)\) is the correct answer.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
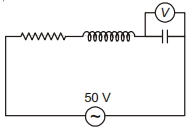
- 1અનુનાદ સમયે આકૃતિમાં દર્શાવેલ વોલ્ટમીટર $V$ નું વાંચન $200\,V$ છે, તો પરિપથનો $Q$ ફેકટર .................. છે.View Solution
- 2$10\,Hz$ આવૃત્તિ અને $12\,V$ ના $r.m.s.$ મૂલ્યના સાઈનોસોડલ પ્રાપ્તિસ્થાનને $2.1\; \mu F$ કેપેસિટર સાથે જોડેલ છે. વિદ્યુતપ્રવાહનું $r.m.s.$ મૂલ્ય $..........mA$ છે.View Solution
- 3$A.C.$ નું $D.C.$ માં રૂપાંતર કરવાની પ્રક્રિયાને શું કહેવાય?View Solution
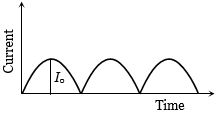
- 4View Solutionરેક્ટિફાયરમાં આઉટપુટ પ્રવાહ અને સમયનો આલેખ આપેલ છે,તો આઉટપુટનું સરેરાશ ...... .
- 5$LCR$ શ્રેણી પરિપથને $sin$ વિધેય પર આધારિત અને મહત્તમ મૂલ્ય $283\, V$ ધરાવતા અને $320/s$ ની કોણીય આવૃતિ ધરાવતા સ્ત્રોત સાથે જોડેલ છે. પરિપથમાં $R\, = 5\,\Omega $ , $L\,= 25\, mH$ અને $C\, = 1000\, \mu F$ છે. પરિપથનો કુલ ઇમ્પીડન્સ અને સ્ત્રોતનાં વૉલ્ટેજ અને પ્રવાહ વચ્ચેનો કળા તફાવત અનુક્રમે કેટલો મળે?View Solution
- 6એક ઇન્ડક્ટર $(20\, mH)$, એક કેપેસિટર $(120\, \mu F)$ અને અવરોધ $(60\,\Omega)$ ધરાવતા એક શ્રેણી $AC$ પરિપથ એ એક $24\, V/50\, Hz$ ના $AC$ ઉદગમથી ચાલીત છે. આ પરિપથમાં $60\, s$માં થતો ઊર્જાનો વ્યય ________ હશે.View Solution
- 7$0.5\,mH$ ના ઈન્ડકટર, $20\,\mu F$ નો સંધારક, અને $20\,\Omega$ ના અવરોધને $220\,V$ ના $ac$ ઉદગમ સાથે શ્રેણીમાં જોડવામાં આવે છે. જો પ્રવાહ $emf$ સાથે કળામાં હોય, તો પરિપથમાં પ્રવાહનો કંપવિસ્તાર $\sqrt{x} \, A$ મળે છે. $x$ નું મૂલ્ય $.............$ થશે.View Solution
- 8$250\, V , 50\, Hz$ ના $AC$ ઉદગમ માથી $LR$ પરિપથ $400\, W$ પાવર વાપરે છે. પરિપથનો પાવર ફેક્ટર $0.8$ છે. પાવર ફેક્ટર $1$ કરવા માટે કેપેસિટર ઉમેરવામાં આવે છે. કેપેસિટર નું મૂલ્ય $\left(\frac{ n }{3 \pi}\right) \mu F ,$ હોય તો $n=$.......View Solution
- 9લિસ્ટ$-I$ ને લિસ્ટ$-II$ સાથે જોડો.View Solution
લિસ્ટ$-I$ લિસ્ટ$-II$ $(a)$ $\omega L\,>\,\frac{1}{\omega C}$ $(i)$ પ્રવાહ $emf$ સાથે કળામાં છે $(b)$ $\omega {L}=\frac{1}{\omega {C}}$ $(ii)$ પ્રવાહ લગાવેલ $emf$ ની પાછળ હોય $(c)$ $\omega {L}\, < \,\frac{1}{\omega {C}}$ $(iii)$ મહત્તમ પ્રવાહ પસાર થાય. $(d)$ અનુનાદ આવૃતિ $(iv)$ પ્રવાહ $emf$ ની આગળ હોય આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 10$AC$ પરિપથમાં વોલ્ટેજ $V$ અને પ્રવાહ $I$ હોય, તો પરિપથનો પાવર વ્યય કેટલો થાય?View Solution
