Download App
નીચે જણાવેલ લોજીક પરિપથ માટે સત્યાર્થ સારણી (ટૂથ ટેબલ) નીચે ....... મુજબ હશે.
  • A
    $A$ $B$ $Y$
    $0$ $0$ $0$
    $0$ $1$ $1$
    $1$ $0$ $1$
    $1$ $1$ $0$
  • B
    $A$ $B$ $Y$
    $0$ $0$ $1$
    $0$ $1$ $0$
    $1$ $0$ $0$
    $1$ $1$ $1$
  • C
    $A$ $B$ $Y$
    $0$ $0$ $1$
    $0$ $1$ $0$
    $1$ $0$ $1$
    $1$ $1$ $0$
  • D
    $A$ $B$ $Y$
    $0$ $0$ $0$
    $0$ $1$ $1$
    $1$ $0$ $0$
    $1$ $1$ $1$
JEE MAIN 2021, Diffcult
Download our app for free and get startedPlay store
b
\(y=\overline{(A \bar{B}+\bar{A} B)}\)

\(y=\overline{A \bar{B}} \cdot \overline{\bar{A} B}\)

\(y=(\bar{A}+B) \cdot(A+\bar{B})\)

\(y=\bar{A} \cdot A+\bar{A} \bar{B}+A \cdot B+B \bar{B}\)

\(y=A B+\bar{A} \bar{B}\)

\(A\) \(B\) \(Y = AB +\overline{ A } \overline{ B }\)
\(0\) \(0\) \(1\)
\(0\) \(1\) \(0\)
\(1\) \(0\) \(0\)
\(1\) \(1\) \(1\)
art

Download our app
and get started for free

Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Download App

Similar Questions

  • 1
    કોમન એમિટર ટ્રાન્ઝિસ્ટર એમ્પ્લિફાયરમાં કલેકટર વચ્ચે વોલ્ટેજ $3\;V $ છે. કલેકટર અવરોધ $3\,k\Omega $ છે. જો પ્રવાહ ગેઇન $100$ અને બેઝ અવરોધ $2\,k\Omega $ હોય, તો એમ્પ્લિફાયરનો વોલ્ટેજ અને પાવઇ ગેઇન કેટલો થાય?
    View Solution
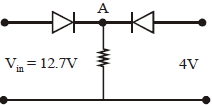
  • 2
    પરિપથમાં દર્શાવેલ બંને ડાયોડ આદર્શ છે અને જ્યારે તે ફોરવર્ડ બાયસમાં જોડાયેલા હોય ત્યારે તેનો અવરોધ અવગણ્ય છે.દરેક ડાયોડનો મૂળભૂત વૉલ્ટેજ (પોટેન્શિયલ બેરિયર) $0.7\; \mathrm{V}$ છે. પરિપથમાં દર્શાવેલ ઈનપુટ વૉલ્ટેજ માટે બિંદુ $A$ નો વૉલ્ટેજ ($Volts$ માં) કેટલો હશે?
    View Solution
  • 3
    ધાતુ અને અર્ધધાતુમાં તાપમાનમાં ફેરફાર કરતાં તેના અવરોધમાં થતો ફેરફાર કોના કારણે હોય છે?
    View Solution
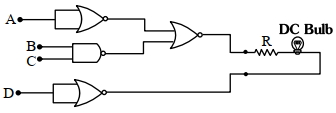
  • 4
    નીચે દર્શાવેલ ગેટ-નો ભાગ પૂર્ણ અનુકૂળ પરિપથમાં જોડવામાં આવેલ છે. નીચે આપેલા ક્યા સંયોજન માટે બલ્બ પ્રજ્વલિત $(\mathrm{ON})$ થશે?
    View Solution
  • 5
    કયા પદાર્થમાં ઊર્જાનો બૅન્ડગૅપ મહત્તમ હોય છે ?
    View Solution
  • 6
    નીચે આપેલી ક્યાં પ્રકારમાં ટ્રાન્ઝીસ્ટર માટે પાવર ગેઈન મહતમ હશે ?
    View Solution
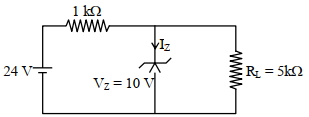
  • 7
    આપેલ પરિપથ માટે ઝેનર ડાયોડની ફરતે પાવર ($mW$ માં) કેટલો હશે?
    View Solution
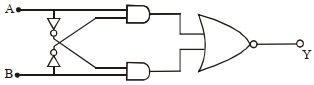
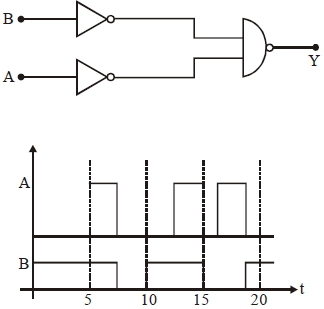
  • 8
    $A$ અને $B$ ઈનપુટ માટે આઉટપુટ $Y$ 
    View Solution
  • 9
    $npn$ ટ્રાન્ઝિસ્ટરથી કોમન એમ્પિયર એમ્પ્લિફાયર બનાવવામાં આવે છે, ઈનપૂટ અવરોધ $100\, \Omega,$ આઉટપુટ અવરોધ $10\, K \Omega$ અને પાવરગેઇન $10^{6}$ હોય તો પ્રવાહગેઇન ' $\beta$ ' શું થશે?
    View Solution
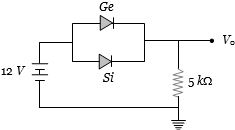
  • 10
    સિલિકોન $Si$  અને જર્મેનિયમ $ Ge$  ડાયોડના કટ-ઇન વોલ્ટેજ અનુક્રમે $0.7 V $ અને $0.3 V$  છે.જર્મેનિયમ ડાયોડને ઉલટાવવાથી $V_o$ માં કેટલા ....$V$ ફેરફાર થાય?
    View Solution