નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
| સ્ટેપ |
Rate constant $\left(\sec ^{-1}\right)$ |
Activation energy $\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$ |
| $1$ | ${k}_1$ | $300$ |
| $2$ | ${k}_2$ | $200$ |
| $3$ | ${k}_3$ | $\mathrm{Ea}_3$ |
ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).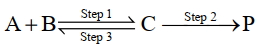
JEE MAIN 2024, Medium
Download our app for free and get started
c
$\mathrm{K}=\frac{\mathrm{K}_1 \mathrm{~K}_2}{\mathrm{~K}_3}$
$\mathrm{K}=\frac{\mathrm{K}_1 \mathrm{~K}_2}{\mathrm{~K}_3}$
$A \mathrm{e}^{\frac{-\mathrm{E}_2}{\mathrm{RT}}}=\frac{\mathrm{A}_1 \mathrm{e}^{\frac{-\mathrm{E}_{\mathrm{a}_1}}{\mathrm{RT}}} \mathrm{A}_2 \mathrm{e}^{\frac{-\mathrm{E}_{2_2}}{\mathrm{RT}}}}{\mathrm{A}_3 \mathrm{e}^{\frac{-\mathrm{E}_{\mathrm{a}_1}}{\mathrm{RT}}}}$
$A \mathrm{e}^{\frac{-\mathrm{E}_2}{\mathrm{RT}}}=\frac{\mathrm{A}_1 \mathrm{~A}_2}{\mathrm{~A}_3} \mathrm{e}^{\frac{-\left(\mathrm{E}_{\mathrm{a}_2}+\mathrm{E}_{\mathrm{a}_2}-\mathrm{E}_{\mathrm{E}_3}\right)}{\mathrm{RT}}}$
$\mathrm{E}_{\mathrm{a}}=\mathrm{E}_{\mathrm{a}_1}+\mathrm{E}_{\mathrm{a}_2}-\mathrm{E}_{\mathrm{a}_3}$
$400=300+200-\mathrm{E}_{\mathrm{a}_3}$
$\mathrm{E}_{\mathrm{a}_3}=100 \mathrm{~kJ} / \mathrm{mole}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$A_2 + B_2 $ $\rightleftharpoons$ $ 2AB $ પુરોગામી અને પ્રતિવર્તીં પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા અનુક્રમે $180\, kJ$ મોલ $^{-1}$ અને $200 \,kJ$ મોલ $^{-1}$ છે. ઉદ્દીપકની હાજરીમાં (પુરોગામી અને પ્રતિવર્તીં) બંનેની સક્રિયકરણ ઊર્જા $100\, kJ$ મોલ $^{-1}$ ઘટે છે તો ઉદ્દીપકની હાજરીમાં ($A_2 + B_2 \rightarrow2AB$) પ્રક્રિયાનો એન્થાલ્પી ફેરફાર ( $kJ $ મોલ $ ^{-1}$) કેટલો થશે?View Solution
- 2View Solutionજુદા-જુદા પ્રક્રિયકો ધરાવતી પ્રક્રિયા કદાપી...... ન હોઈ શકે ?
- 3અર્ધ આયુષ્યના કિરણોત્સર્ગી નમૂના માટે ત્વરિત સમયે કિરણોત્સર્ગી વિઘટનનો દર$2.2 \times 10^{9}\; \mathrm{s}$$10^{10} \;\mathrm{s}^{-1}$છે .તે ઇન્સ્ટન્ટમાં તે નમૂનામાં કિરણોત્સર્ગી અણુઓની સંખ્યા કેટલી છે ?View Solution
- 4પ્રથમ ક્રમના વાયુના તબક્કાની પ્રક્રિયા માટે:View Solution
$A _{( g )} \rightarrow 2 B _{( g )}+ C _{( g )}$
$A$ અને $P _{ t }$ નું પ્રારંભિક દબાણ $P _{0}$ છે $'t'$ સમયે કુલ દબાણ એકીકૃત દર સમીકરણ શું હશે ?
- 5જો પ્રક્રિયક $ B$ ની સાંદ્રતા બમણી થાય તો પ્રક્રિયક $A$ અને $B$ વચ્ચેની પ્રક્રિયાનો દર પ્રારંભિક દર $1/4$ જેટલો થાય છે. પ્રક્રિયક $B$ ના સંદર્ભમાં પ્રક્રિયાનો ક્રમ ...... થશે.View Solution
- 6આપેલ આલેખ બે જુદી જુદી પ્રક્રિયા $(i)$ અને $(ii)$ માટે સમય સાથે પ્રક્રિયક $R$ ની સાંદ્રતાનો ફેરફાર રજૂ કરે છે. તી પ્રક્રિયાના ક્રમ અનુક્રમે જણાવો.View Solution
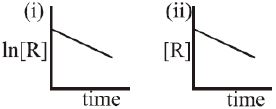
- 7$A + B \rightarrow C + D$ માટે $\Delta H = -\,20\,kj $ મોલ $^{-1} $ છે. પુરોગામી પ્રક્રિયાની સક્રિયકરણ ઊર્જા $85\,KJ$ મોલ $^{-1}$ છે. તો પ્રતિગામી પ્રક્રિયા માટે સક્રિયકરણ ઊર્જા......... $KJ$ મોલ $^{-1}$ છે.View Solution
- 8અચળ ક્દે વાયુ $A$ નાં પ્રથમ ક્રમના ઉષ્મીય વિઘટન દરમિયાન નીચે મુજબ માહિતી પ્રાપ્ત થાય છે.View Solution
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$S.\ No$ સમય/s કુલ દબાણ/(atm)
$1.$ $0$ $0.1$
$2.$ $115$ $0.28$
પ્રક્રિયાનો વેગ અચળાંક _______________$\times 10^{-2} \mathrm{~s}^{-1}$ (નજીકનાં પૂનાંકમાં)
- 9$A \rightarrow P$ પ્રથમ ક્રમની પ્રક્રિયા માટે, તાપમાન $(T)$ આધારે દર અચળાંક $(k)$ નીચેના સમીકરણ $\log \,k = \, - (2000)\,\frac{1}{T}+ 0.6$ પર આધારિત છે. તો પૂર્વ ઘાતાંકીય ગુણાંક $A$ અને સક્રિયકરણ ઊર્જા $E_a$ અનુક્રમે... થાય.View Solution
- 10જો ક્ષય અચળાંક $K=$ ${\text{1}}{\text{.155}} \times {\text{1}}{{\text{0}}^{{\text{ - 3}}}}$ સેકન્ડ હોય તો પ્રથમ ક્રમમાં પ્રક્રિયા આપનારી પ્રક્રિયાઓની સાંદ્રતા ......... સેકન્ડ પછી અડધી થઈ જશેView Solution