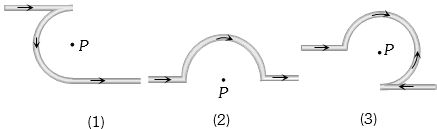
(a) Case \(1\) : \({B_A} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r} \otimes \)
\({B_B} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{r}\odot\)
\({B_C} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}\odot\)
So net magnetic field at the centre of case \(1\)
\({B_1} = {B_B} - {B_C} - {B_A} \Rightarrow {B_1} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi i}}{r}\odot\)..... \((i)\)
Case \(2\) : As we discussed before magnetic field at the centre \(O\) in this case
\({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi i}}{r} \otimes \) ..... \((ii)\)
Case \(3\) : \({B_A} = 0\) \({B_B} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{(2\pi - \pi /2)i}}{r} \otimes \)
\({B_C} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}\odot\)
\( = \frac{{{\mu _0}}}{{4\pi }}.\frac{{3\pi i}}{{2r}} \otimes \)
So net magnetic field at the centre of case \(3\) \({B_3} = \frac{{{\mu _0}}}{{4\pi }}.\frac{i}{r}\left( {\frac{{3\pi }}{2} - 1} \right) \otimes \)..... \((iii)\)
From equation \((i)\), \((ii)\) and \((iii)\)
\({B_1}:{B_2}:{B_3} = \pi \odot\) : \(\pi \otimes \) \(\left( {\frac{{3\pi }}{2} - 1} \right)\, \otimes = - \frac{\pi }{2}:\frac{\pi }{2}:\left( {\frac{{3\pi }}{4} - \frac{1}{2}} \right)\)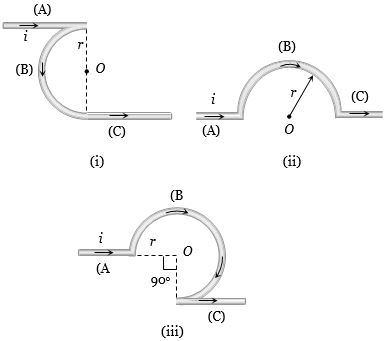
Download our appand get started for free
Similar Questions
- 1સમાન ગતિઊર્જા ધરાવતા બે વિદ્યુતભારિત કણો ગતિની દિશાને લંબરૂપે રહેલા નિયમિત ચુંબકીય ક્ષેત્રમાંથી પસાર કરાવવામાં આવે છે. જે તેમના વર્તુળાકાર પથોની ત્રિજ્યાઓનો ગુણોત્તર $6: 5$ હોય અને તેમના દળોનો ગુણોત્તર $9: 4$ હોય, તો તેમના પરના વીજભારોનો ગુણોત્તર $......$ થશે.View Solution
- 2$2.5 \times {10^7}\,m/s$ ના વેગથી ગતિ કરતો એક પ્રોટોન $2.5\,T$ ધરાવતા ચુંબકીયક્ષેત્રમાં ${30^o}$ ના ખૂણે દાખલ થાય છે. તો પ્રોટોન પર લાગતું બળ કેટલું હશે?View Solution
- 3$(i)$ પ્રવાહધારિત કોઇલની ચુંબકીય મોમેન્ટ એ ત્રિજ્યાના ક્યા પ્રમાણમાં છે?View Solution
- 4પ્રોટોન અને $\alpha$ ની ગતિઉર્જા $K _{ p }$ અને $K _{\alpha}$ છે. તે ચુંબકીયક્ષેત્રમાં લંબ દાખલ થતાં ત્રિજ્યાના ગુણોતર $2: 1 $ છે તો ગતિઉર્જાનો ગુણોતર $K _{ p }: K _{\alpha}$ શું હશેView Solution
- 5$50\, keV$ ની ગતિઊર્જા ધરાવતો ડયુટેરોન $\overrightarrow B$ ચુંબકીયક્ષેત્રને લંબ સમતલમાં $0.5\;m$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં ગતિ કરે છે. સમાન સમતલમાં સમાન $\overrightarrow B$ ચુંબકીયક્ષેત્રમાં $0.5\;m$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં પ્રોટોનની ગતિઊર્જા ......$keV$ થાય?View Solution
- 6$100$ આંટા અને $1 \,cm^2 $ ક્ષેત્રફળ ધરાવતા ગેલ્વેનોમીટરના કોઇલનો વળઅચળાંક $10^{-8 }\, N-m\, rad.$ છે.જો ચુંબકીયક્ષેત્ર $5 \,T$ હોય,તો પ્રવાહસંવેદીતા કેટલી થાય?View Solution
- 7અતિ લાંબા સોલેનોઇડના અક્ષ પર ઉદ્ભવતું ચુંબકીયક્ષેત્ર $B$ છે. જો તેમાંથી વહેતો પ્રવાહ બમણો તથા એકમ લંબાઇદીઠ આંટાઓની સંખ્યા અડઘી કરવામાં આવે,તો અક્ષ પર નવું ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 8$\alpha$ કણ અન પ્રોટોન સમાન વેગથી સમાન ચુંબકીય ક્ષેત્રને લંબરૂપે દાખલ થતાં તેના વર્તુળાકાર પથની ત્રિજ્યાનો ગુણોતર ..... .View Solution
- 9ટોરોઈડમાં એકમ લંબાઈ દીઠ આંટાઓની સંખ્યા $1000$ છે અને તેમાંથી પસાર થતો વિદ્યુતપ્રવાહ $\frac{1}{4 \pi}$ એમ્પિયર છે. અંદરની બાજુએ ઉત્પન્ન થતું ચુંબકીય ક્ષેત્ર $\left(\right.$વેબર/ $\left.m ^2\right)$ માં કેટલું હશે ?View Solution
- 10બે લાંબા પાતળા $d$ અંતરે રહેલા સમાંતર તારમાંથી સમાન દિશામાં $i$ જેટલો પ્રવાહ વહેતો હોય તો ....View Solution
