નીચેની માહિતી પરથી નાઇટ્રિક ઓક્સાઇડની સર્જન એન્થાલ્પી કેટલા .......$kJ\,mo{l^{ - 1}}$ થશે ?$N{O_{\left( g \right)}} + C{O_{\left( g \right)}} \to 1/2{N_{2\left( g \right)}} + C{O_{2\left( g \right)}};\Delta {H^o} = - 372.2\,kJ/mol$
$\Delta H_f^o\left( {CO} \right) = - 110.5\,kJ\,mo{l^{ - 1}};$
$\Delta H_f^o\left( {C{O_2}} \right) = - 393.5\,kJ\,mo{l^{ - 1}}$
Medium
Download our app for free and get started
b
\(NO + CO \longrightarrow \frac{1}{2} N _2+ CO _2\)
\(NO + CO \longrightarrow \frac{1}{2} N _2+ CO _2\)
\(\Delta H ^{\circ}=\left|\frac{1}{2} \Delta_1 H _{ N _2}^{\circ}+2 \Delta_1 H _{ CO _2}^{\circ}\right|-\left|\Delta_1 H _{ NO }^{\circ}+\Delta_1 H _{ CO }^{\circ}\right|\)
\(-372.2=\left|\frac{1}{2}(0)+(-393.5)\right|-\left|\Delta_1 H _{ NO }^0+(-110.5)\right|\)
\(\therefore \Delta_1 H _{ NO }^{\circ}=-393.5+110.5+372.2=-393.5+482.7\)
\(=89.2\, kJ\, mol ^{-1}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉષ્મા એન્જિન તાપમાન ${T_1}$ પર ઉષ્મા ${Q_1}$ શોષે છે અને તાપમાન ${T_2}$ પર ${Q_2}$ ઉષ્મા શોષી લે છે. એન્જિન દ્વારા કરવામાં આવેલ કાર્ય $({Q_1} + {Q_2})$ છે. આ માહિતિ પરથી,..View Solution
- 2એક મોલ પ્રવાહી સ્વરૂપ પાણીનું વરાળમાં રૂપાંતર કરતા $373 \,K$ તાપમાને એન્ટ્રોપી ફેરફાર ...... જૂલ/કેલ્વિન ($\Delta S$ (બાષ્પાયન) $= 2.257$ કિલોજૂલ/ગ્રામ)View Solution
- 3View Solutionઅચળ દબાણમાં બરફ સાથે સંતુલનમાં પાણીની મોલર ઉષ્મા ક્ષમતા છે
- 4નીચે બે પ્રક્રિયાઓ આપેલ છે.View Solution
$2 \mathrm{Fe}_{(\mathrm{s})}+\frac{3}{2} \mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{Fe}_2 \mathrm{O}_{3(\mathrm{~s})}, \Delta \mathrm{H}^{\mathrm{o}}=-822 \mathrm{~kJ} / \mathrm{mol}$
$\mathrm{C}_{(\mathrm{s})}+\frac{1}{2} \mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{CO}_{(\mathrm{g})}, \Delta \mathrm{H}^{\mathrm{o}}=-110 \mathrm{~kJ} / \mathrm{mol}$
$3\mathrm{C}_{(\mathrm{s})}+\mathrm{Fe}_2 \mathrm{O}_{3(\mathrm{~s})} \rightarrow 2 \mathrm{Fe}_{(\mathrm{s})}+3 \mathrm{CO}_{(\mathrm{g})}$ આપેલા પ્ર્ક્રિયા માટે એન્થાલ્પી ફેરફાર__ _ _$J/mol$ છે.
- 5એક બોમ્બ કેલોરીમીટરમાં, સાયનામાઈડ $NH _{2} CN _{( s )}$ અને ઓકિસજનની પ્રક્રિયા કરવામાં આવે છે અને તેનો $\Delta U -742.24\, kJ\, mol ^{-1}$ માલૂમ પડયો. તો આપેલી પ્રક્રિયા માટે,View Solution
$NH _{2} CN _{( s )}+\frac{3}{2} O _{2}( g ) \rightarrow N _{2( g )}+ O _{2}( g )+ H _{2} O _{(l)}$
$\Delta H _{298}$ ની માત્રા ........ $kJ$ છે. (નજીક પૂર્ણાંક રાઉન્ડ ઓફ)
[ધારી લો આદર્શ વાયુઓ અને $\left. R =8.314\, J\, mol ^{-1} K ^{-1}\right]$
- 6$25^o$ બોમ્બ કેલેરી મીટરમાં ઈથેનોલની દહન ઉષ્મા $-670.48\, K.$ કેટલી મોલ$^{-1}$ છે. તો આ પ્રક્રિયા માટે $25\,^oC$ એ $\Delta$$H$ નું મૂલ્ય કેટલા .....$K.\, Cals.$ ?View Solution
- 7ઓટોમોબાઈલમાં થતી નીચેની પ્રક્રિયા માટે $\Delta H, \Delta S, \Delta G$ નાં મૂલ્યો અનુક્રમે ...... હોય છે.View Solution
$2C_8H_{18}$ $_{(g)}$ + $25O_2$ $_{(g)}$ $\rightarrow$ $16CO_2$$_{(g)}$ + $18H_2O$ $_{(g)}$
- 8$15.5\, g$ પ્રોપેનના દહનથી કેટલા $.......kJ$ ઉષ્મા ઉત્પન્ન થાય ? ${C_3}{H_8} + 5{O_2} \to 3C{O_2} + 4{H_2}O\,;\,\Delta {H^o} = - 2219\,kJ/mol$View Solution
- 9આપેલ આક્રૂતિને ધ્યાનમાં લો.View Solution
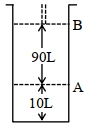
$18^{\circ} \mathrm{C}$ પર, સ્થાન $A$ પર, પિસ્ટન સાથે જોડેલા (fitted) સિલિન્ડર માં આદર્શ વાયુનો $1$ $\mathrm{mol}$ રાખેલ છે. જો તાપમાન માં કોઈપણ જાતનો ફેરફાર ન કરીએ તો પિસ્ટન એ સ્થાન $B$ તરફ ખસે છે ત્યારે આ પ્રતિવર્તી પ્રક્રમ માં થયેલ કાર્ય $'x' L atm$ છે. $x=-$ ........... $L.atm$ (નજીક નો પૂર્ણાક)
[આપેલ : નિરપેક્ષ તાપમાન $={ }^{\circ} \mathrm{C}+273.15, \mathrm{R}=0.08206 \mathrm{~L} \mathrm{~atm} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ ]
- 10View Solutionકઈ પ્રક્રિયામાં એન્ટ્રોપી વધે છે ?