નિયમિત રીતે વિદ્યુતભારીત કરેલા ગોળામાં વિદ્યુતભાર ઘનતા $r =R$ સુધી નીચેના સૂત્ર વડે અપાય છે. $\rho (r)=\;\rho _0\left( {\frac{5}{4} - \frac{r}{R}} \right)$, $r > R$ માટે $\;\rho $ $(r)=0 $ છે.જયાં,$r$ એ કેન્દ્રથી અંતર છે.કેન્દ્રથી $r$ અંતરે $(r < R) $ વિદ્યુતક્ષેત્રની તીવ્રતા ________
AIEEE 2010, Diffcult
c
Let us consider a spherical shell of radius \(x\) and thickness \(dx\)
Let us consider a spherical shell of radius \(x\) and thickness \(dx\)
Charge on this shell
\(d q=\rho \cdot 4 \pi x^{2} d x=\rho_{0}\left(\frac{5}{4}-\frac{x}{R}\right) .4 \pi x^{2} d x\)
\(\therefore\) Total charge in the spherical region from centre to \(r\) \((r < R)\) is
\(q=\int d q=4 \pi \rho_{0} \int_{0}^{r}\left(\frac{5}{4}-\frac{x}{R}\right) x^{2} d x\)
\(=4 \pi \rho_{0}\left[\frac{5}{4} \cdot \frac{r^{3}}{3}-\frac{1}{R} \cdot \frac{r^{4}}{4}\right]=\pi \rho_{0} r^{3}\left(\frac{5}{3}-\frac{r}{R}\right)\)
Electric field at \(r, E=\frac{1}{4 \pi \epsilon_{0}} \cdot \frac{q}{r^{2}}\)
\(=\frac{1}{4 \pi \epsilon_{0}} \cdot \frac{\pi \rho_{0} r^{3}}{r^{2}}\left(\frac{5}{3}-\frac{r}{R}\right)=\frac{\rho_{0} r}{4 \epsilon_{0}}\left(\frac{5}{3}-\frac{r}{R}\right)\)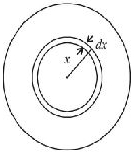
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$q$ વિદ્યુતભાર ધરાવતા બે ધન આયનો વચ્ચેનું અંતર $d $ છે. જો તેમની વચ્ચેનું અપાકર્ષણ બળ $F $ હોય, તો દરેક આયન પર ખૂટતાં ઇલેકટ્રોનની સંખ્યા કેટલી હશે? ($e$ ઇલેક્ટ્રોન પરનો વિદ્યુતભાર છે)View Solution
- 2$R$ ત્રિજયાના ગોળાના કેન્દ્રથી અંતર નો વિદ્યુતક્ષેત્ર $E$ વિરુધ્ધનો આલેખ કેવો થાય?View Solution
- 3$0.1 \,\mu m$ ત્રિજ્યાનો એક વિદ્યુતભારતીત પાણીનું ટીપુ વિદ્યુતક્ષેત્રની સંતુલન અવસ્થા હેઠળ આવેલ છે. ટીપા પરનો વિદ્યુતભાર ઈલેકટ્રોનીક્સ વિદ્યુતભારને સમતુલ્ય છે. વિદ્યુતક્ષેત્રની તીવ્રતા ........$N/C$ છે.View Solution
- 4$10\, mg$ દળ ધરાવતાં બે નાના ગોળાઓને $0.5\, m$ લંબાઈની દોરી દ્વારા એક બિંદુ પરથી લટકાવવામાં આવ્યા છે. બંને પર એક સરખો વિજભાર છે અને એકબીજાને $0.20\, m$ અંતર સુધી અપાકર્ષિત કરે છે. દરેક ગોળા પરનો વિજભાર $\frac{ a }{21} \times 10^{-8} \, C$ છે તો $a$ નું મૂલ્ય ........ હશે. [$g=10 \,ms ^{-2}$ આપેલ છે. ]View Solution
- 5$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 6ઉગમબિંદુ $O$ આગળ તેના કેન્દ્ર સાથે $X - Y$ સમતલમાં $R$ ત્રિજ્યાની ધન વિદ્યુતભારીત પાતળી ધાતુની રીંગ નિયત કરેલી છે. બિંદુ $(0, 0, Z_0)$ આગળ એક ઋણ વિદ્યુતભારીત કણ $P$ ને સ્થિર સ્થિતિએથી છોડવામાં આવે છે. જ્યાં $(Z_0 > 0)$ તો ગતિ છે.View Solution
- 7$R$ ત્રિજયાવાળી પોલી સપાટીમાં $Q$ કુલંબ વિદ્યુતભાર રહેલો છે. જો સપાટીની ત્રિજયા બમણી કરતા સપાટી સાથે સંકળાયેલ ફલક્સ .....View Solution
- 8આકૃતિમાં $A$ આગળના વિદ્યુતભાર પરનું બળ $BC$ ને લંબ દિશામાં ...... હશે.View Solution
- 9$25.5\, k\,Vm^{-1}$ જેટલા વિદ્યુતક્ષેત્રમાં $6$ વધારાના ઇલેક્ટ્રોન ધરાવતા પ્રવાહીના ટીપાને સ્થિર રાખવામા આવે છે.પ્રવાહીની ઘનતા $1.26\times10^3\, kg\, m^{-3}$ હોય તો ટીપાની ત્રિજ્યા કેટલી હશે?View Solution
- 10વિદ્યુતક્ષેત્ર ને $(6 \hat{i}+5 \hat{j}+3 \hat{k}) \mathrm{N} / \mathrm{C}$ વડે આપવામાં આવે છે. $YZ$ સમતલમાં રહેલા $30 \hat{i} \mathrm{~m}^2$ જેટલું ક્ષેત્રફળ ધરાવતી સપાટીમાંથી પસાર થતું વિદ્યુત ફલકસ $SI$ એકમમાં ________ થશે.View Solution
