$ ({\pi ^2}) $ લંબાઇ અને $2\,A$ પ્રવાહધારિત તારથી $1\,cm$ અંતરે ચુંબકીયક્ષેત્ર $B_1$ છે.હવે તારને વર્તુળાકારમાં વાળતાં કેન્દ્ર પર ચુંબકીયક્ષેત્ર $B_2$ છે.તો $ \frac{{{B_2}}}{{{B_1}}} =$
Medium
b
(b) If a wire of length \(l\) is bent in the form of a circle of radius \(r\) then \(2\pi r = l\) \(==>\) \(r = \frac{l}{{2\pi }}\)
\(\vec F = i(\vec L \times \vec B)\)
Magnetic field due to straight wire \({B_1} = \frac{{{\mu _0}}}{{4\pi }} \cdot \frac{{2i}}{r} = \frac{{{\mu _0}}}{{4\pi }} \times \frac{{2 \times 2}}{{1 \times {{10}^{ - 2}}}}\)
(b) If a wire of length \(l\) is bent in the form of a circle of radius \(r\) then \(2\pi r = l\) \(==>\) \(r = \frac{l}{{2\pi }}\)
\(\vec F = i(\vec L \times \vec B)\)
Magnetic field due to straight wire \({B_1} = \frac{{{\mu _0}}}{{4\pi }} \cdot \frac{{2i}}{r} = \frac{{{\mu _0}}}{{4\pi }} \times \frac{{2 \times 2}}{{1 \times {{10}^{ - 2}}}}\)
also magnetic field due to circular loop \({B_2} = \frac{{{\mu _0}}}{{4\pi }} \cdot \frac{{2\pi i}}{r} = \frac{{{\mu _0}}}{{4\pi }} \cdot \frac{{2\pi \times 2}}{{\pi /2}}\)
\(==>\) \(\frac{{{B_2}}}{{{B_1}}} = \frac{1}{{50}}\)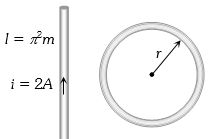
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો $R$ ત્રિજ્યાના $A$ વર્તુળાકાર ગુચળામાં $I$ વિદ્યુત પ્રવાહ વહેતું હોય અને બીજા $2R$ ત્રિજ્યાના $B$ ગૂચળામાં $2I$ પ્રવાહ વહેતો હોય તો તેમના દ્વારા ઉદ્ભવતા ચુંબકીય ક્ષેત્ર $B_A$ અને $B_B$ નો ગુણોત્તર શું થાય?View Solution
- 2એક લાંબી, સુરેખ અને પાતળી દિવાલવાળી પાઇપમાંથી વિદ્યુતપ્રવાહ $I$ વહે છે. તો નીચેનામાંથી ક્યું વિધાન સાયું છે?View Solution
- 3$2 \times 10^{-3} \mathrm{~T}$ નું સમાન ચુંબકીયક્ષેત્ર ધન $\mathrm{Y}$ અક્ષની દિશામાં અસ્તિત્વ ધરાવે છે. $\mathrm{Y}-\mathrm{Z}$ સમતલમાં રહેલ $20 \mathrm{~cm}$ અને $10 \mathrm{~cm}$ લંબાઈની બાજુ ધરાવતી એક લંબચોરસ લુપ માંથી $5$ $A$ વિદ્યુત પ્રવાહ પસાર થાય છે. આ ગુંચળામાં ઋણ $\mathrm{X}$ અક્ષના સંદર્ભમાં વિષમઘડી દિશામાં વિદ્યુત પ્રવાહ વહે છે. તો આ ગૂંચળા પર લાગતા ટોર્કનું મૂલ્ય અને દિશા ...View Solution
- 4$R$ ત્રિજ્યાની અવાહક તકતી પર $Q$ વિદ્યુતભાર નિયમિત રીતે વહેંચાયેલો છે. તકતીના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબરૂપે રહેલી અક્ષને અનુલક્ષીને તકતી $\omega$ જેટલી કોણીય ઝડપથી પરિભ્રમણ કરે છે. જેને કરાણે તકતીના કેન્દ્ર પર $B$ જેટલું ચુંબકીય ક્ષેત્ર પ્રેરિત થાય છે. હવે જે વિદ્યુતભાર અને કોણીય ઝડપને અચળ રાખીએ અને તકતીની ત્રિજ્યાને બદલાતી લઈએ તો તક્તીના કેન્દ્રમાં ચુંબકીય પ્રેરણ નીચેના પૈકી કઈ આકૃતિ પ્રમાણે બદલાશે?View Solution
- 5સમાન ગતિઊર્જા ધરાવતા બે વિદ્યુતભારિત કણો ગતિની દિશાને લંબરૂપે રહેલા નિયમિત ચુંબકીય ક્ષેત્રમાંથી પસાર કરાવવામાં આવે છે. જે તેમના વર્તુળાકાર પથોની ત્રિજ્યાઓનો ગુણોત્તર $6: 5$ હોય અને તેમના દળોનો ગુણોત્તર $9: 4$ હોય, તો તેમના પરના વીજભારોનો ગુણોત્તર $......$ થશે.View Solution
- 6ચલિત ગૂંચળાના ગેલ્વેનોમીટરમાં $24 \Omega$ નો શંટ લગાડતા તેનું આવર્તન $25$ કાપામાંથી $5$કાપા જેટલું ધટે છે. ગેલ્વેનોમીટરના ગૂંચળાનો અવરોધ_________હશે.View Solution
- 7$5\,cm$ ત્રિજ્યા ધરાવતા અને એકદદમ નજીક-નજીક વીંટળાયેલા વર્તુળાકાર ગૂંચળા (ગાળા) ને કારણે તેના કેન્દ્ર આગળ $37.68 \times 10^{-4}\,T$ જેટલું ચુંબકીયક્ષેત્ર ઉત્પન્ન થાય છે. ગૂંચળાંમાંથી વહેતો પ્રવાહ $..........\;A$ છે. [ધારો કે આંટાની સંખ્યા $100$ છે અને $\pi=3.14$ ]View Solution
- 8$l$ લંબાઈના સાદા લોલકમાં એક છેડે લોખંડનો ગોળો લટકાવેલો છે.આ લોલક $d.c.$ પ્રવાહ ધરાવતા સમક્ષિતિજ ગૂચળાની ઉપર દોલનો કરે છે તો લોલકનો આવર્તકાળ $T$ ......View Solution
- 9View Solutionએક વિદ્યુતભારિત કણ ચુંબકીય ક્ષેત્રને લંબ ગતિ કરે છે, તો .....
- 10$q$ વિદ્યુતભાર અને $m$ દળ ધરાવતો કણ $x-$ અક્ષની દિશામાં $v$ વેગથી ગતિ કરે છે.તો કઇ આકૃતિમાં કણ પર લાગતું બળ શૂન્ય થાય?View Solution
