પ્લેટોની વચ્ચે હવાનું માધ્યમ ધરાવતા સમાંતર પ્લેટ કેપેસિટરનું કેપેસિટન્સ $9\ pF$ છે. પ્લેટો વચ્ચેનું અંતર $'d'$ છે. હવે પ્લેટોની વચ્ચેની જગ્યાને ડાય-ઈલેકટ્રીક વડે ભરવામાં આવે છે. જેમાં એક ડાઈ ઈલેકટ્રીક પાસે $ K_1 = 3$ અને ડાઈ ઈલેકટ્રીક અચળાંક અને જાડાઈ $d$ છે. જ્યારે બીજા પાસે ડાઈ ઈલેકટ્રીક અચળાંક $K_2 = 6$ અને જાડાઈ $2d/3$ છે. તો હવે, કેપેસિટરનું કેસિટન્સ ......$pF$ શોધો.
Medium
c
\(C = \frac{{{ \in _0}\,A}}{d}\,\, = \,9\,PF\)
\(C = \frac{{{ \in _0}\,A}}{d}\,\, = \,9\,PF\)
\(\,{C_1}\,\, = \,\,\frac{{{ \in _0}\,{K_1}A}}{{d/3}}\,\, = \,\,3{K_1}\,\,\frac{{{ \in _0}A}}{d}\,\, = \,\,3\,\, \times \,\,3\,\, \times \,\,9\, = \,\,81\,\,pF\)
\({C_2}\,\, = \,\,\frac{{{ \in _0}{k_2}\,A}}{{2d/3}}\,\, = \,\,\frac{3}{2}\,\,{K_2}\,\,\frac{{{ \in _0}A}}{d}\,\, = \,\,\frac{3}{2}\,\, \times \,\,6\,\, \times \,\,9\,\, = \,\,81\,\,pF\)
જેમ \(C_1\) અને \(C_2\) શ્રેણીમાં જોડેલ છે.
\({C_3}\,\, = \,\,\frac{{{C_1}{C_2}}}{{{C_1}\,\, + \;\,{C_2}}}\,\, = \,\,\frac{{81\,\, \times \,\,81}}{{81\,\, + \;\,81}}\,\, = \,\,\frac{{81\,\, \times \,\,81}}{{162}}\,\, = \,\,40.5\,\,pF\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$C_1 = 1\,\mu F$ કેપેસિટરને મહતમ $V_1 = 6\, KV$ અને $C_2 = 3\,\mu F$ કેપેસિટરને મહતમ $V_2 = 4\,KV$ વોલ્ટેજ આપી શકીએ છીએ. જો બંને કેપેસિટરને શ્રેણીમાં લગાવીએ તો તેને મહતમ કેટલા........$KV$ વોલ્ટેજ આપવા જોઇએ?View Solution
- 2બે સમકેન્દ્રિય ગોળીય કવચથી કેપેસિટર બનાવવામાં આવે છે, ${R_1}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_1}$ અને ${R_2}$ ત્રિજયાવાળી ગોળીય કવચનો વોલ્ટેજ ${V_2}$ છે,તો કેન્દ્રથી $x$ અંતરે આવેલા બિંદુએ વોલ્ટેજ કેટલો થાય? (${R_2} > x > {R_1}$)View Solution
- 3$0.02 \,m$ ની ત્રિજ્યા અને દરેક $5 \mu C$ વીજભાર ધરાવતા યોંસઠ $(64)$ ટીપાં જોડાઈને એક મોટુ ટીપું બનાવે છે. મોટાં ટીપાં અને નાનાં ટીપાંની પૃષ્ઠ ધનતાનો ગુણોત્તર ............... થશે.View Solution
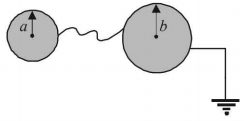
- 4$a$ અને $b$ ત્રિજ્યાના બે સુવાહક કવચને વાયર વડે જોડેલ છે. આ તંત્રની કેપેસિટી $..........$View Solution
- 5એક સમાંતર પ્લેટ સંધારકને $10$ જેટલો ડાયઈલેક્ટિક અચળાંક ધરાવતા માધ્યમ થી ભરવામાં આવે છે અને બેટરી સાથે જોડી વીજભારિત કરવામાં આવે છે. આ ડાયઈલેક્ટ્રિક ચોસલાને બીજા $15$ ડાયઈલેક્ટ્રિક અચળાંક ઘરાવતા ચોસલા વડે બદલવામાં આવે છે. તો સંધારકમાં ઊર્જા ............View Solution
- 6View Solutionકેપેસિટરને બેટરી વડે ચાર્જ કરેલ છે.હવે બેટરી દૂર કરીને બીજા સમાન વિદ્યુતભારરહિત કેપેસિટર સાથે સમાંતરમાં જોડવામાં આવે છે. તંત્રની કુલ સ્થિતવિદ્યુતઊર્જા .....
- 7પ્લેટોની વચ્ચે $K$ ડાય-ઈલેકટ્રીક અચળાંક ધરાવતા ડાય ઈલેકટ્રીક સાથે એક સમાંતર પ્લેટ સંગ્રાહકની કેપેસિટી $C$ અને $A$ ને $V$ વોલ્ટ સ્થિતિમાન સુધી ચાર્જ કરેલ છે. પ્લેટો વચ્ચે ડાઈ ઈલેકટ્રીન સ્લેબને ધીમે ધીમે દૂર કરવામાં આવે છે અને ત્યારબાદ ફરી દાખલ કરવામાં આવે છે. આ પ્રક્રિયા તંત્ર દ્વારા થતું ચોખ્ખું કાર્ય.....View Solution
- 8બે બિંદુઓ $P$ અને $Q$ પાસે વિદ્યુતસ્થિતિમાનો અનુક્રમે $10\ V$ અને $-4\ V$ છે તો $100$ ઈલેક્ટ્રોનને $P$ થી $Q$ પર લઈ જવા કરવું પડતું કાર્ય ........View Solution
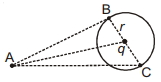
- 9$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
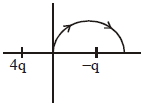
- 10$x-$અક્ષ પર $4 q$ અને $-q$ વિજભાર ધરાવતા બે બિંદુવત વિજભાર $x=-\frac{d}{2}$ અને $x=\frac{d}{2}$ સ્થાને જડેલ છે. જો ત્રીજા $'q'$ જેટલા બિંદુવત વિજભારને આકૃતિમાં દર્શાવ્યા પ્રમાણે ઉગમબિંદુથી $x = d$ સુધી અર્ધવર્તુળાકાર માર્ગ પર લઈ જવામાં આવે છે. તો તે દરમિયાન વિજભારની ઉર્જા....View Solution