$0.02 \,m$ ની ત્રિજ્યા અને દરેક $5 \mu C$ વીજભાર ધરાવતા યોંસઠ $(64)$ ટીપાં જોડાઈને એક મોટુ ટીપું બનાવે છે. મોટાં ટીપાં અને નાનાં ટીપાંની પૃષ્ઠ ધનતાનો ગુણોત્તર ............... થશે.
JEE MAIN 2022, Medium
b
Let \(R=\) radius of combined drop
Let \(R=\) radius of combined drop
\(r=\) radius of smaller drop
Volume will remain same
\(\frac{4}{3} \pi R ^{3}=64 \times \frac{4}{3} \pi r ^{3}\)
\(R =4 r\)
\(Q =64 q ;\)
\(q\) : charge of smaller drop
\(Q\) : Charge of combined drop
\(\frac{\sigma_{\text {bigger }}}{\sigma_{\text {smaller }}}=\frac{\frac{ Q }{4 \pi R ^{2}}}{\frac{ q }{4 \pi r ^{2}}}=\frac{ Q }{ q } \cdot \frac{ r ^{2}}{ R ^{2}}\)
\(=64 \frac{ r ^{2}}{16 r ^{2}}=4\)
\(\frac{\sigma_{\text {bigger }}}{\sigma_{\text {smaller }}}=\frac{4}{1}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
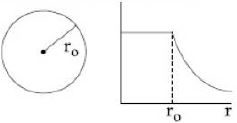
- 1આપેલ આલેખ _____ નો ફેરફાર (કેન્દ્રથી $r$ અંતર સાથે) દર્શાવે છે.View Solution
- 2વિદ્યુતભારિત સંધારકની બે પ્લેટો વચ્ચે રહેલા વિદ્યુતભારિત કણ પર $10 \,N$ નું બળ લાગે છે. ને સંધારકની કોઈ એક પ્લેટ દૂર કરવામાં આવે તો તે કણ ઉપર લાગતું બળ .......... $N$View Solution
- 3$0.2\,F$ કેપેસિટરને $600\,V$ ની બેટરી સાથે જોડેલ છે.હવે બેટરી દૂર કરીને $1\,F$ ના કેપેસિટર સાથે જોડતાં, નવો વોલ્ટેજ કેટલા........$volts$ થાય?View Solution
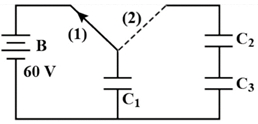
- 4જ્યારે કળ $(1)$ જોડેલી હોય ત્યારે $V\, = 60\,V$ બેટરી $B$ વડે $C_1$ કેપેસીટરને ચાર્જ કરવામાં આવે છે.જ્યારે કળ $(2)$ બંધ કરવામાં આવે ત્યારે બે વિજભારરહિત કેપેસીટર $C_2\, = 3.0\,\mu F$ અને $C_3\,= 6.0\,\mu F$ સાથે આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડવામાં આવે છે. $C_2$ અને $C_3$ પર અંતિમ કુલ વિજભાર $\mu C$માં કેટલો મળે?View Solution
- 5સમાંતર પ્લેટ કેપેસીટરમાં $A$ સપાટીનું ક્ષેત્રફળ ધરાવતી બે પ્લેટ $d$ અંતરે છે.જેને ડાઈઇલેક્ટ્રિકથી ભરવામાં આવે છે . જેની પરમિટિવિટી એક પ્લેટ આગળ ${ \varepsilon _1}$ અને બીજી પ્લેટ આગળ ${ \varepsilon _2}$ છે તો આ કેપેસીટરનું કેપેસીટન્સ કેટલું હશે?View Solution
- 6$8\,\mu F,\;250\, V$ ના કેપેસિટરથી $16\,\mu F,\;1000\, V$ નું કેપેસિટર બનાવવા માટે કેટલા કેપેસિટરની જરૂર પડશે?View Solution
- 7આકૃતિમાં દર્શાવ્યા પ્રમાણે સાત એકસરખા ક્ષેત્રફળ $A$ ધરાવતી પ્લેટો $d$ જેટલા અંતરે રહેલી છે. આ સ્થિતિમાં બિંદુ $P$ અને $Q$ વચ્ચેનો અસરકારક કેપેસીટન્સ કેટલો થશે?View Solution

- 8$R$ ત્રિજયા ધરાવતી બે પ્લેટને $d$ અંતરે મૂકતાં કેપેસિટન્સ $C$ બને છે.હવે $R/2$ ત્રિજયા ધરાવતો અને $d$ જાડાઇ ધરાવતો ડાઇઇલેકિટ્રક $6$ ને મૂકતાં નવું કેપેસિટન્સ કેટલુ થાય?View Solution
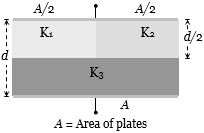
- 9સમતુલ્ય ડાઇઇલેકિટ્રક અચળાંક $k$ હોય,તો..View Solution
- 10કેપેસિટરનો વોલ્ટેજ $5\ V$ થી $10\ V$ કરવા માટે $W$ કાર્ય કરવું પડે છે,તો વોલ્ટેજ $10\ V$ થી $15\ V$ કરવા માટે કેટલા.......$W$ કાર્ય કરવું પડે?View Solution
