$ I= \frac{1}{{\sqrt 2 }} sin \left( {100\pi t} \right)$
$E=\frac{1}{\sqrt{2}} \sin (100 \pi t+\pi / 3)$
આ પરિપથમાં થતો સરેરાશ પાવર વ્યય વોટમાં કેટલો હશે?
\(\text { Given }: i=\frac{1}{\sqrt{2}} \sin (100 \pi t) \text { ampere }\)
Compare it with \(i=i_{0} \sin (\omega t),\) we get
\(i_{0}=\frac{1}{\sqrt{2}} \mathrm{A}\)
Given \(: e=\frac{1}{\sqrt{2}} \sin \left(100 \pi t+\frac{\pi}{3}\right)\) volt
Compare it with, we get
\(e_{0}=\frac{1}{\sqrt{2}} V, \phi=\frac{\pi}{3}\)
\(\therefore i_{\mathrm{rms}}=\frac{i_{0}}{\sqrt{2}}=\frac{\frac{1}{\sqrt{2}}}{\sqrt{2}} \mathrm{A}=\frac{1}{2} \mathrm{A}\)
\(e_{\mathrm{rms}}=\frac{e_{0}}{\sqrt{2}}=\frac{\frac{1}{\sqrt{2}}}{\sqrt{2}} \mathrm{V}=\frac{1}{2} \mathrm{V}\)
Average power consumed in the circuit,
\(P = {i_{rms}}\,{e_{ems}}\,\cos \,\phi \)
\(=\left(\frac{1}{2}\right)\left(\frac{1}{2}\right) \cos \frac{\pi}{3}=\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{1}{8} \,\mathrm{W}\)
Download our appand get started for free
Similar Questions
- 1શુદ્ધ (ફકત) અવરોધ ધરાવતા પરિપથ ધટક $X$ને $100\,V$ મહત્તમ વોલ્ટેજ ધરાવતા $a.c.$ ઉદગમ સાથે જોડવામાં આવે છે ત્યારે તે $5A$ નો મહત્તમ પ્રવાહ આપે છે, કે જે વોલ્ટેજ સાથે કળામાં છે. જ્યારે બીજા પરિપથ ધટક $Y$ને આ જ $a.c.$ ઉદગમ સાથે જોડવામાં આવે છે ત્યારે તે પણ સમાન મહત્તમ પ્રવાહ આપે છે. પણ તે કળામાં વોલ્ટેજ કરતાં $\frac{\pi}{2}$ પાછળ છે. જો $X$ અને $Y$ ધટકોને આ જ ઉદગમ સાથે શ્રેણીમાં જોડવામાં આવે છે તો પ્રવાહનું $rms$ મૂલ્ય એમ્પિયરમાં કેટલું હશે ?View Solution
- 2View Solutionખોટું વિધાન પસંદ કરો.
- 3$A.C.$ વોલ્ટેજ $E = 141\sin (628\,t),$ હોય,તો $ r.m.s$ મૂલ્ય અને આવૃત્તિ કેટલી થાય?View Solution
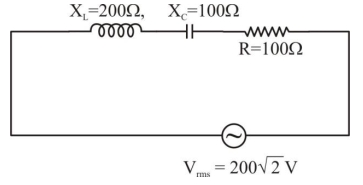
- 4$ac$ પરિપથમાં પ્રત્યાવર્તી વોલ્ટેજ, $e=200 \sqrt{2} \sin 100 t$ વોલ્ટને $1 \;\mu F$ના કેપેસીટન્સ ધરાવતા કેપેસિટર સાથે જોડેલ છે. આ પરિપથમાં પ્રવાહનું $rms$ મૂલ્ય ($mA$ માં) કેટલું હશે?View Solution
- 5$40\, \Omega$ ના અવરોધને $220 \,V , 50\, Hz$ નું રેટીગ ધરાવતા ઉલટસૂલટ પ્રવાહ ઉદગમ સાથે જોડાવામાં આવેલ છે. પ્રવાહને તેના મહત્તમ મૂલ્યથી $rms$ મૂલ્ય જેટલું થવા માટે લાગતો સમય...... હશે.View Solution
- 6અવરોધ અને કેપેસિટરને શ્રેણીમાં જોડીને $\omega $ કોણીય આવૃત્તિ ધરાવતા $AC$ ઉદ્ગમ સાથે જોડવામાં આવે છે,વોલ્ટેજ અચળ રાખીને આવૃત્તિ $\omega /3$ કરતાં પ્રવાહ અડધો થાય છે,તો શરૂઆતની આવૃત્તિએ રીએકટન્સ અને અવરોધનો ગુણોત્તર કેટલો થાય?View Solution
- 7એક આર્ક બલ્બને પ્રકાશીત થવા $10$ $A$ $DC$ અને $80$ $V$ ની આવશ્યકતા છે.જો આ બલ્બને $220$ $V$ $(rms)$,$50$ $Hz$ $AC$ સપ્લાય સાથે જોડવામાં આવે તો, તેને પ્રકાશીત કરવા જરૂરી શ્રેણી ઇન્ડકટરનું મૂલ્ય લગભગ થશે.View Solution
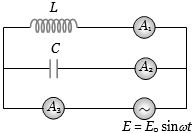
- 8આકૃતિમાં બતાવ્યા અનુસાર ઇન્ડક્ટર $ L $ અને કેપેસિટર $ C $ સર્કિટમાં જોડાયેલ છે. વીજ પુરવઠાની આવર્તન સર્કિટની રેઝોન્ટ આવર્તન સમાન છે. કયુ એમીટર ઝીરો એમ્પીયર વાંચશે?View Solution
- 9એસી પરિપથમાં પાવર ફેકટર $\frac{1}{3}$ થી $\frac{1}{9}$ બદલાય છે, તો જો અવરોધ અચળ રહે તો રિએેકટન્સ કેટલી ટકાવારીથી બદલાશે (અંદાજિત)View Solution
- 10આપેલ પરિપથમાં અવરોધમાંથી પસાર થતા પ્રવાહનું $rms$ મૂલ્ય ( $\left.I _{ rms }\right)$ $...........\,A$View Solution