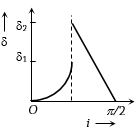
પ્રકાશનું કિરણ $\mu$ વક્રીભવનાંક ધરાવતા માધ્યમમાંથી હવામાં ગતિ કરે છે.તા વિચલનકોણ ($\delta$ ) અને આપાતકોણ $(i)$ નો આલેખ કેવો થાય?
Diffcult
a
\((a)\)The ray of light is refracted at the plane surface. However, since the ray is travelling from a denser to a rarer medium, for an angle of incidence \((i)\) greater then the critical angle \((c)\) the ray will be totally internally reflected.
\((a)\)The ray of light is refracted at the plane surface. However, since the ray is travelling from a denser to a rarer medium, for an angle of incidence \((i)\) greater then the critical angle \((c)\) the ray will be totally internally reflected.
\((1)\) For \(i < c\); deviation = \(r -i\) with \(\frac{1}{\mu } = \frac{{\sin i}}{{\sin r}}\)
Hence \(\delta = {\sin ^{ - 1}}\left({\mu \sin i} \right) - i\)
This is a non-linear relation. The maximum value of
\(\delta\) is \({\delta _1} = \frac{\pi }{2} - c\); where \( i = c\) and \(\mu = \frac{1}{{\sin c}}\)
\((2)\) For \(i > c\), deviation \(\delta\) = \(\pi\) -\(2i\)
\(\delta\) decreases linearly with \(i\)
\(\delta_2=\pi -2 c= 2 \delta_1\)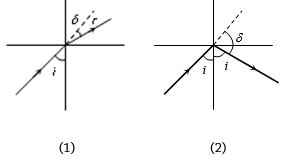
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\,cm $ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાથી કેટલે દૂર પદાર્થ મૂકતાં પ્રતિબિંબ બમણાં આકારનું મળશે?View Solution
- 2એક પેપરને પાણી ભરેલા ગ્લાસની નીચે મૂકવામાં આવે છે. જ્યાં પાણી અને ગ્લાસનો વક્રીભવનાંક અનુક્રમે $1.5$ અને $1.33$ છે. જો ગ્લાસના તળિયાની જાડાઈ $1\, cm$ અને ભરેલા પાણીની ઊંડાઈ $5\, cm$ હોય તો ઉપરથી જોતાં કાગળ કેટલું શીફ્ટ થયેલું દેખાશે?View Solution
- 3પ્રિઝમનો પ્રિઝમકોણ $60^o $ અને વક્રીભવનાંક $\sqrt 2 $ હોય,તો લઘુત્તમ વિચલનકોણ .......$^o$ થાય?View Solution
- 4હવામાં પ્રકાશની તરંગલંબાઇ $4200\, \mathring A$ હોય,તો પાણી $(\mu = 4/3)$ માં પ્રકાશની તરંગલંબાઇ કેટલા .....$\, \mathring A$ થાય?View Solution
- 5પ્રકાશ હવામાંથી આપેલા માધ્યમમાં હવા-માધ્યમ આંંતર પૃષ્ઠ સાથે $45^{\circ}$ ના કોણે દાખલ થાય છે. વક્રીભવન અનુભવ્યા બાદ પ્રકાશ કિરણ તેની મૂળ દિશાથી $15^{\circ}$ ના કોણે વિચલન અનુભવે છે.માધ્યમનો વક્રીભવનાંક $........$ થશે.View Solution
- 6એક ફિલન્ટનાં અને બીજા ક્રાઉન કાચનાં બે પ્રિઝમોનું સંયોજન વિચલન વગર વિભાજન ઉત્પન્ન કરે છે. ફિલન્ટ કાચના પ્રિઝમનો કોણ $15^o$ છે. લાલ અને જાંબલી રંગ માટે ચોખ્ખું કોણીય નિયોજન ..... હશે. અહીં વિચલન માટે (ક્રાઉન કાચ માટે $\mu = 1.52$, ક્રાઉન કાચ માટે $\mu =1.65,$ ક્રાઉન કાચ માટે $\omega =0.20$, ફિલન્ટ કાચ માટે $\omega =0.03$).View Solution
- 7એસ્ટ્રોનોમિકલ ટેલિસ્કોપમાં ઓબ્જિેકિટવપીસ અને આઇપીસ ની કેન્દ્રલંબાઇ $60cm$ અને $10cm$ છે. તો મોટવણી કેટલી થાય?View Solution
- 8View Solutionટ્રાવેલિંગ માઇક્રોસ્કોપ દ્વારા એક કાચના સ્લેબનો વક્રીભવનાંકમાપવામાં આવે છે તો તે માટે ઓછામાં ઓછા કેટલા અવલોકનોની જરૂર પડશે?
- 9પ્રકાશ $M_1$ અને $M_2$ એમ બે માધ્યમોમાં અનુક્રમે $1.5 \times 10^8 ms ^{-1}$ અને $2.0 \times 10^8 ms ^{-1}$ ની ઝડપ સાથે ગતિ કરે છે. તેઆની વચ્ચેનો કાંતિકોણ $...........$ થશે.View Solution
- 10View Solutionપ્રકાશ હવામાંથી કાંચમાં દાખલ થાય ત્યારે...