પ્રક્રિયાક્રમ વિશે નીચેના પૈકી કયું વિધાન સાચું છે?
Medium
Download our app for free and get started
b
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપ્રક્રિયાના ક્રમ માટે કયું વિધાન ખોટું છે ?
- 2$aG + bH \rightarrow$ નિપજ પ્રક્રિયાને ધ્યાનમાં લેતાં જ્યારે $G$ અને $H$ બંને પ્રક્રિયકોની સાંદ્રતા બમણી હોય તો દર વધીને $8$ ગણું થાય છે. જો કે જ્યારે $G$ ની સાંદ્રતા બમણી થાય ત્યારે $H$ ની સાંદ્રતા નિયત રહે તો દર બમણો થશે. તો સમગ્ર પ્રક્રિયાનો ક્રમ શું થશે?View Solution
- 3પ્રથમ ક્રમની એક પ્રકિયા $15\,\min$ માં $75\%$ પૂર્ણ થાય, તો પ્રક્રિયાને $90\%$ પૂર્ણ થતા ........... $\min$ લાગશે.View Solution
- 4$A \rightarrow B$ પ્રથમ ક્રમની પ્રક્રિયા માટે $0.01\,M$ પ્રક્રિયકની સાંદ્રતાની પ્રક્રિયા દર $2.0 \times 10^{-5} $ મોલ $L^{-1}\,S^{-1} $ છે. તો પ્રક્રિયાનો અદ્ય આયુ ........ સેકન્ડ છે.View Solution
- 5$A + 2B $ $\rightleftharpoons$ $ 2C + D$ પ્રક્રિયામાં $A$ ની સાંદ્રતા ચાર ગણી વધે અને $B$ ની સાંદ્રતા ઘટીને અડધી થાય તો પ્રક્રિયાનો દર = ........View Solution
- 6${A} \rightarrow {B}$ પ્રક્રિયા માટે, દર અચળાંક ${k}$ એ ${s}^{-1}$માં $\log _{10} {k}=20.35-\frac{\left(2.47 \times 10^{3}\right)}{{T}}$ દ્વારા આપવામાં આવે છે. સક્રિયકરણની ઊર્જા $.....$ ${kJ} \,{mol}^{-1}$ છે. (નજીકના પૂર્ણાંકમાં) $\left[\right.$ આપેલ છે $\left.: {R}=8.314\, {~J}\, {~K}^{-1}\, {~mol}^{-1}\right]$View Solution
- 7મોટા ભાગની પ્રક્રિયાનો તાપમાન ગુણાંક $.......$ ની વચ્ચે હોય છે.View Solution
- 8પ્રથમક્રમની એક પ્રક્રિયા $45$ મિનિટમાં અડધી પૂર્ણ થાય છે. તો આ પ્રક્રિયાને $99.9\%$ પૂર્ણ થતાં ......... કલાક લાગે.View Solution
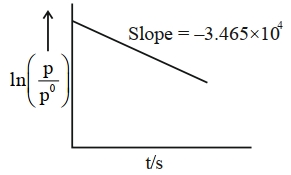
- 9એઝોમિથેનના વિધટન માટે,View Solution
$CH _3 N _2 CH _3( g ) \rightarrow CH _3 CH _3( g )+ N _2( g )$
આ એક પ્રથમક્રમ પ્રક્રિયા છે. $600\, K$ પર સમય સાથે આંશિક દબાણમાં વિવિધતા નીચે આપેલ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય $\times 10^{-5}\, s$ છે. [નજીકનો પૂર્ણાંક]
- 10અહીં પ્રથમ ક્રમ પ્રક્રિયા માટે તેના $1\,M$ થી $0.6 \,M$ સુધી તેને $20$ મિનિટ લાગે છે. તો $0.6 \,M$ થી $0.36\, M$ સાંદ્રતા સુધી પહોચતા કેટલો સમય જરૂરી છે.View Solution