પૃથ્વી પર નિષ્ક્રમણ વેગ $(v_e)$ તથા ગ્રહ પર નિષ્ક્રમણ વેગ $(v_p)$ નો ગુણોત્તર કેટલો હશે? ગ્રહની ત્રિજયા અને સરેરાશ ઘનતા, પૃથ્વીની સરેરાશ ઘનતા કરતાં બે ગણી છે.
NEET 2016, Medium
Download our app for free and get started
a
As escape velocity, \(v = \sqrt {\frac{{2GM}}{R}} \)
As escape velocity, \(v = \sqrt {\frac{{2GM}}{R}} \)
\( = \sqrt {\frac{{2G}}{R}\frac{{4\pi {R^3}}}{3}\rho } = - R\sqrt {\frac{{8\pi G}}{3}\rho } \)
\(\therefore \frac{{{v_e}}}{{{v_p}}} = \frac{{{R_e}}}{{{R_p}}} \times \sqrt {\frac{{{\rho _e}}}{{{\rho _p}}}} = \frac{1}{2} \times \sqrt {\frac{1}{2}} = \frac{1}{{\underline {2\sqrt 2 } }}\)
\(\left( {{R_p} = 2{R_e}and\,{\rho _p} = 2{\rho _e}} \right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વીના કેન્દ્રથી અંતર $d$ સાથે ગુરુત્વપ્રવેગ $g$ માં થતા બદલાવને શ્રેષ્ઠ રીતે રજુ કરે છે. ($ R=$ પૃથ્વીની ત્રિજયા)View Solution
- 2View Solutionજ્યાં ગુરુત્વસ્થિતિમાન શૂન્ય હોય ત્યાં ...
- 3પૃથ્વીની સપાટી થી $1000 \,km$ ઉપર રહેલા વાતાવરણીય કણને નિષ્ક્રમણ વેગ ..... $km / s$ છે. (પૃથ્વીની ત્રિજ્યા $6400 \,km$ અને $g=9.8 \,m / s ^2$ છે.)View Solution
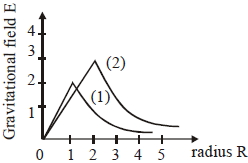
- 4$\mathrm{R}_{1}=1 \;\mathrm{m}$ અને $\mathrm{R}_{2}=2\; \mathrm{m}$ ત્રિજ્યા અને $\mathrm{M}_{1}$ અને $\mathrm{M}_{2}$ દળ ધરાવતા બે ગોળા માટે ગુરુત્વાકર્ષી ક્ષેત્રનો ગ્રાફ આપેલ છે તો $\frac{\mathrm{M}_{1}}{\mathrm{M}_{2}}$ નો ગુણોત્તર કેટલો થાય?View Solution
- 5$A$ અને $B$ ગ્રહ ની ત્રિજ્યાનો ગુણોત્તર ${k_1}$ અને ગુરુત્વપ્રવેગનો ગુણોત્તર ${k_2}$ હોય તો નિષ્ક્રમણ ઝડપ નો ગુણોત્તર કેટલો થાય?View Solution
- 6જો પૃથ્વી પર ગુરુત્વ પ્રવેગ $10 m/s^2 $ હોય તો પૃથ્વી ના કેન્દ્ર પર ગુરુત્વ પ્રવેગ કેટલો થાય?( પૃથ્વીની ત્રિજ્યા$=R$ )View Solution
- 7પૃથ્વીનું દળ $6.00 \times {10^{24}}\,kg$ અને ચંદ્ર નું દળ $7.40 \times {10^{22}}\,kg$. ગુરુત્વાકર્ષણનો અચળાંક $G = 6.67 \times {10^{ - 11}}\,N - {m^2}/k{g^2}$. જો તંત્રની ગુરુત્વસ્થિતિઉર્જા $ - 7.79 \times {10^{28}}\,joules$ છે. તો ચંદ્ર અને પૃથ્વી વચ્ચેનું અંતર કેટલું હશે?View Solution
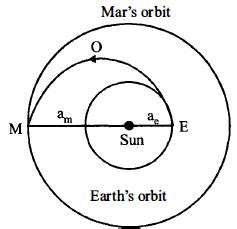
- 8ભારતના મંગળયાનને મંગળ પર મોકલવા માટે સૂર્યની ફરતે ફરતી $EOM$ કક્ષામાં દાખલ કરવામાં આવે છે.જે પૃથ્વી પરથી $E$ બિંદુથી નીકળે છે અને $M$ બિંદુ આગળ મંગળને મળે છે.જો પૃથ્વીની કક્ષાની અર્ધ-પ્રધાન અક્ષ $a_e = 1.5 \times 10^{11}\, m$, અને મંગળની કક્ષાની અર્ધ-પ્રધાન અક્ષ $a_m= 2.28 \times 10^{11}\, m$ છે. કેપલરના નિયમનો ઉપયોગ કરીને મંગળયાનને પૃથ્વી પરથી મંગળ પર પહોચવા ........ $(days)$ સમય લાગશે.View Solution
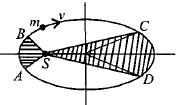
- 9આકૃતિ સૂર્યની આસપાસ $m$ ગ્રહની દીર્ઘવૃતિય કક્ષા બતાવેલ છે $S$. $SDC$ દ્વારા ઘેરાતું ક્ષેત્રફળ $SAB$ દ્વારા ઘેરાતા ક્ષેત્રફળ કરતા બમણું છે. જો ગ્રહને $C$ થી $D$ જવા માટે લાગતો સમય $ t_1$ અને $A$ થી $B $ જવા માટે લાગતો સમય $t_2$ હોય, તોView Solution
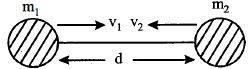
- 10બે કાલ્પનિક $m_1$ અને $m_2$ દળ ધરાવતા ગ્રહ એક બીજાથી અનંત અંતરે છે.હવે ગુરુત્વાકર્ષણને કારણે તેમના કેન્દ્રને જોડતી રેખા પર તે એકબીજા તરફ ગતિ કરે છે.જ્યારે તેમની વચ્ચેનું અંતર $d$ હોય ત્યારે તેમની ઝડપ કેટલી હશે? $(m_1$ ની ઝડપ $v_1$ અને $m_2$ ની ઝડપ $v_2$ છે $)$View Solution
