પૃથવીને પોતાની ધરી પર કેટલા કોણીય વેગ થી ભ્રમણ કરવી જોવે કે જેથી વિષુવવૃત પર વજન અત્યારના વજન કરતાં $3/5 $ ગણું થાય? . (પૃથ્વીની ત્રિજ્યા $6400\, km$)
Medium
Download our app for free and get started
c
(c) Weight of the body at equator = \(\frac{3}{5}\) of initial weight
(c) Weight of the body at equator = \(\frac{3}{5}\) of initial weight
\(g' = \frac{3}{5}g\) (because mass remains constant)
\(g' = g - {\omega ^2}R{\cos ^2}\lambda \) \(⇒\) \(\frac{3}{5}g = g - {\omega ^2}R{\cos ^2}(0^\circ )\)
\(⇒\) \({\omega ^2} = \frac{{2g}}{{5R}}\) \(⇒\) \(\omega = \sqrt {\frac{{2g}}{{5R}}} = \sqrt {\frac{{2 \times 10}}{{5 \times 6400 \times {{10}^3}}}} \) = \(7.8 \times {10^{ - 4}}\frac{{rad}}{{\sec }}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી પૃથ્નીની સપાટી ઉપરથી, સપાટીથી $2 R$ ઉંચાઈએ વર્તુળાકાર કક્ષામાં $m$ દળ ધરાવતા ઉ૫ગ્રહને તરતો મૂક્વા માટે જરૂરી લધુતમ ઊર્જા. . . . . . . . છે.View Solution
- 2જો પૃથ્વી $R$ ત્રિજ્યાનો ગોળો હોય અને $g_{30}$ એ $30^o $ અક્ષાંશ પર ગુરુત્વ પ્રવેગ અને $g $ એ વિષુવવૃત પરનો પ્રવેગ તો $g - g_{30}$ નું મૂલ્ય કેટલું થાય?View Solution
- 3View Solutionગુરુત્વાકર્ષણ અચળાંક એ શેના પર આધાર રાખે છે ?
- 4એક કુત્રિમ ઉપગ્રહ એ પૃથ્વીની આસપાસ વર્તુળાકાર કક્ષામાં તેની પૃથ્વી પરથી નિષ્ક્રમણ ઝડપ કરતાં પાંચમાં ભાગ જેટલી ઝડપ સાથે પરિભ્રમણ કરી રહ્યું છે તો તેની પૃથ્વીની સપાટીથી ઊંચાઈ શું હશે ? ($R$ પૃથ્વીની ત્રિજ્યાં છે.)View Solution
- 5પૃથ્વીની સપાટી પર $g$ નું મૂલ્ય $980 cm/sec^2 $ તો $64\, km$ ઊંચાઈએ $g$ નું મૂલ્ય ........ $cm/{\sec ^2}$ થાય? (પૃથ્વી નીં ત્રિજ્યા $R= 6400 \,km$ )View Solution
- 6View Solutionચંદ્ર ને પૃથ્વીના પ્ર્ક્ષિપ્ત ગુરુત્વાકર્ષણ માથી છટકી જવા તેના વેગમાં કેટલા ગણો વધારો કરવો પડે ?
- 7જો એક ઉપગ્રહ પૃથ્વીની ફરતે $r$ ત્રિજયાની ક્ક્ષામાં $v$ વેગથી પરિભ્રમણ કરતો ઉપગ્રહ તેની થોડીક ઉર્જા ગુમાવે તો $r$ અને $v$ માટે શું સાચું છે.View Solution
- 8પૃથ્વીની ત્રિજયા લગભગ $6400\; km$ અને મંગળની ત્રિજયા $3200\; km$ છે. પૃથ્વીનું દળ, મંગળના દળ કરતાં લગભગ $10$ ગણું છે. પૃથ્વીની સપાટી પર કોઇ પદાર્થનું વજન $200 \;N$ છે. મંગળની સપાટી પર તેનું વજન ($N$ માં) કેટલું હશે?View Solution
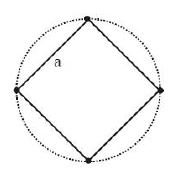
- 9ચાર $M$ દળના કણ $a$ ત્રિજયાના ચોરસના શીરોબિંદુ પર છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે આ કણને બીજા કણોના ગુરુત્વાકર્ષણ ક્ષેત્રને લીધે વર્તુળાકાર કક્ષામાં ભ્રમણ કરતા હોય તો તેનો વેગ કેટલો હશે?View Solution
- 10એક ગ્રહ દીર્ઘવૃતિય કક્ષામાં સૂર્યની આસપાસ ફરે છે. જો $T, V, E$ અને $L$ તેની ગતિ ઊર્જા, ગુરુત્વ સ્થિતિઊર્જા, કુલ ઊર્જા અને કોણીય વેગમાન દર્શાવે છે, નીચે પૈકી શું સાચું થાય?View Solution