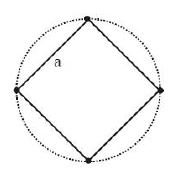
Net force on particle towards center of circle is
\({F_c} = \frac{{G{M^2}}}{{2{a^2}}} + \frac{{G{M^2}}}{{{a^2}}}\sqrt 2 \)
\( = \frac{{G{M^2}}}{{{a^2}}}\left( {\frac{1}{2} + \sqrt 2 } \right)\)
This force will act as centripetal force.
Diatance of particle from center of circle is \(\frac{a}{{\sqrt 2 }}.\)
\(r = \frac{a}{{\sqrt 2 }},{F_c} = \frac{{m{v^2}}}{r}\)
\(\frac{{m{v^2}}}{{\frac{a}{{\sqrt 2 }}}} = \frac{{G{M^2}}}{{{a^2}}}\left( {\frac{1}{2} + \sqrt 2 } \right)\)
\({v^2} = \frac{{GM}}{a}\left( {\frac{1}{{2\sqrt 2 }} + 1} \right)\)
\({v^2} = \frac{{GM}}{a}\left( {1.35} \right)\,\,;\,\,v = 1.16\sqrt {\frac{{GM}}{a}} \)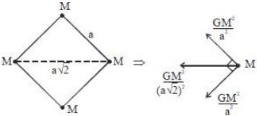
Download our appand get started for free
Similar Questions
- 1એક $M$ દળના રોકેટને પૃથ્વીની સપાટી પરથી શિરોલંબ દિશામાં $V$ વેગથી પ્રક્ષિપ્ત કરવામાં આવે છે. જો પૃથ્વીની ત્રિજ્યા $R$ હોય અને હવાના અવરોધને અવગણવામાં આવે તો રોકેટે પૃથ્વીની સપાટીથી પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ કેટલી હોય ?View Solution
- 2ઉત્તર ધ્રુવ ઉપર એક વસ્તુનું સ્પ્રિંગ કાંટા ઉપર વજન $49\, N$ છે. જે તેને વિષવવૃત્ત ઉપર ખસેડવામાં આવે તો આ જ વજનકાંટા ઉપર તેનું ....... $N$ વજન નોંધાશે ?View Solution
[$g=\frac{G M}{R^{2}}=9.8 \,ms ^{-2}$ લો અને પૃથ્વીની ત્રિજ્યા $R =6400\, km$]
- 3પદાર્થને $2R$ ત્રિજ્યાની ભ્રમણકક્ષા થી $3R$ ત્રિજ્યાની ભ્રમણકક્ષા માં લઈ જવા માટે કેટલુ કાર્ય કરવું પડે?View Solution
- 4$20 \,cm$ બાજુવાળા સમબાજુ ત્રિકોણના શિરોબિંદુ પર $100\,gm$ ના કણો મૂકેલા છે. હવે તેમની વચ્ચેનું અંતર અંનત કરવા કેટલું કાર્ય કરવું પડે?View Solution
- 5બિંદુવત દળને પૃથ્વીની સપાટીથી $h$ ઊંંચાઈએ અને પૃથ્વીની સપાટીથી $\alpha h \left( h \ll < R _{ e }\right)$ જેટલી ઊંંડાઈએ ગુરુત્વાકર્ષણને કારણે ઉત્પન્ન પ્રવેગ સમાન અનુભવાય છે. $\alpha$ નું મૂલ્ય થશે.કારણે ઉત્પન્ન પ્રવેગ સમાન અનુભવાય છે. $\alpha$ નું મૂલ્ય થશે.$\text { ( } R _{ e }=6400\,km)$View Solution
- 6ચંદ્ર કરતાં પૃથ્વી નું દળ $81$ ગણું અને ત્રિજ્યા $3.5$ ગણી હોય તો ચંદ્ર અને પૃથ્વી ના ગુરુત્વ પ્રવેગ નો ગુણોતર કેટલો થાય?View Solution
- 7$1 \,kg$ દળના પદાર્થની નિષ્ક્રમણ ઝડપ $100\, m/sec$ છે .પદાર્થ ની ગ્રહ ની સપાટી પરની ગુરુત્વસ્થિતિઉર્જા ......... $J$ થાય.View Solution
- 8જો પૃથ્વી કોઈ ચાકગતિ કરતું ના હોય તો વિષુવવૃત પાસે એક માણસનું વજન $W$ છે.પૃથ્વીને પોતાની અક્ષની સપેકસે કેટલા કોણીય વેગથી ગતિ કરાવવી જોઈએ કે જેથી માણસનું વજન $\frac{3}{4}\,W$ જેટલું થાય? પૃથ્વીની ત્રિજ્યા $6400\, km$ અને $g = 10\, m/s^2$.View Solution
- 9નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ : જો પૃથ્વીની આજુબાજુ ફરતા ઉપગ્રહની કુલ ઊર્જા $E$ હોય તો તેની સ્થિતિ ઊર્જા $\frac{ E }{2}$ હશે.
વિધાન $II$ : કક્ષામાં ગતિ કરતા ઉપગ્રહની ગતિઊર્જા, કુલ ઊર્જા $E$ ના અડધા મૂલ્ય બરાબર છે.
ઉપરોક્ત વિધાનોના આધારે, નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 10View Solutionકેપ્લરનો બીજો નિયમ કયા નિયમનું વિધાન છે
