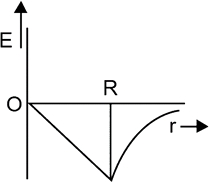
પૃથ્વીની ગુરુત્વક્ષેત્રની તીવ્રતા $(E)$ નો કેન્દ્રથી અંતર $(r)$ પરનો આધાર કયો આલેખ રજૂ કરે છે?
- A
- B
- C
- D
AIPMT 2014, Medium
Download our app for free and get started
a
For a point inside the earth \(i.e.r < R\)
For a point inside the earth \(i.e.r < R\)
\(E = - \frac{{GM}}{{{R^3}}}r\)
Where \(M\) and \(R\) be mass and radius of the earth respectively.
At the center, \(r=0\)
\(\therefore \,E = 0\)
For a point outside the earth \(i.e.\,r > R,\)
\(E = - \frac{{GM}}{{{r^2}}}\)
On the surface of the earth \(i.e.\,r > R,\)
\(E = - \frac{{GM}}{{{R^2}}}\)
The variation of \(E\) with distance \(r\) from the center is as shown in the figure.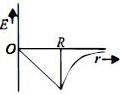
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
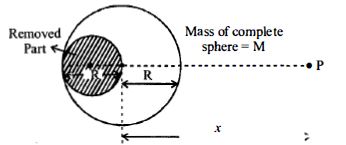
- 1આપેલ ગોળામાં દર્શાવેલ ભાગ કાપી નાખ્યા પછી વધેલા ભાગનું દૂર રહેલા બિંદુ $P$ આગળ ગુરુત્વાકર્ષીક્ષેત્ર કેટલું મળશે?View Solution
- 2એક પદાર્થને પૃથ્વીની સપાટીની ઉપર પૃથ્વીના કેન્દ્રથી $\frac{5}{4}R$ જેટલા અંતરે લઈ જવામાં આવે છે, જ્યાં $R = 6400\,km$ એ પૃથ્વીની ત્રિજ્યા છે. પદાર્થના વજનમાં થતો પ્રતિશત ધટાડો $......\%$ થશે.View Solution
- 3એક કણને પૃથ્વીની સપાટી પરથી શિરોલંબ રીતે ઉપરની તરફ $v=\sqrt{\frac{4 g R_e}{3}}$ વેગ સાથે પ્રક્ષિપ્ત કરવામાં આવે છે. તો કણને તેના દ્વારા મેળવેલી મહત્તમ ઊંચાઈ કરતાં અડધી ઊંચાઈએ વેગ શું હશે?View Solution
- 4કોઈ સ્થાને ગુરુત્વાકર્ષણક્ષેત્ર $\vec E$ $=(5\,N / kg)\, \hat i + (12\,N / kg)\,\hat j$ મુજબ પ્રવર્તે છે.જો કેન્દ્ર આગળ સ્થિતિમાન શૂન્ય લેવામાં આવે તો $(12\,m, 0)$ અને $(0, 5\,m)$ અંતરે રહેલ સ્થિતિમાનનો ગુણોત્તર કેટલો થાય?View Solution
- 5પૃથ્વી (પૃથ્વીનું દળ $M_E$ અને પૃથ્વીની ત્રિજયા $R_E$) ફરતે $3R_E$ ત્રિજયાના $m$ દળનો એક ઉપગ્રહ વર્તુળાકાર કક્ષામાં છે. આ ઉપગ્રહને $9R_E$ ત્રિજયાની કક્ષામાં લઈ જવા માટે વધારાની કેટલી ઊર્જાની જરૂરી પડે?View Solution
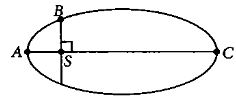
- 6સૂર્યની ફરતે દીર્ઘવૃતિય કક્ષામાં રહેલ ગ્રહની $A,B $ અને $C $ સ્થિતિ પર ગતિઊર્જા અનુક્રમે $K_A,K_B $ અને $K_C$ છે. આકૃતિમાં બતાવ્યા પ્રમાણે, $AC$ મુખ્યઅક્ષ અને $SB$ એ સૂર્યની સ્થિતિ $S$ પર $AC$ ઉપરનો લંબ છે. તોView Solution
- 7જો પૃથ્વી પોતાની અક્ષને ફરતે ભ્રમણ કરવાનું બંધ કરે તો $45^o$ અક્ષાંશ પર $g$ ના મૂલ્યમાં $C.G.S.$ એકમમાં ........ $cm/sec^{2}$ વધારો થાય.View Solution
- 8એક $M$ દળના રોકેટને પૃથ્વીની સપાટી પરથી શિરોલંબ દિશામાં $V$ વેગથી પ્રક્ષિપ્ત કરવામાં આવે છે. જો પૃથ્વીની ત્રિજ્યા $R$ હોય અને હવાના અવરોધને અવગણવામાં આવે તો રોકેટે પૃથ્વીની સપાટીથી પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ કેટલી હોય ?View Solution
- 9કેપ્લરના ત્રીજા નિયમ મુજબ, સૂર્યનું પરિભ્રમણ કરતા ગ્રહનો આવર્તકાળ $(T)$ તે ગ્રહ અને સૂર્ય વચ્ચેના સરેરાશ અંતર $r$ ની ત્રણ ઘાતના સમપ્રમાણમાં છે.View Solution
$\therefore {T^2} = k{r^3}$,
જયાં $K$ અચળાંક છે.
જો સૂર્યનું અને ગ્રહનું દળ અનુક્રમે $M$ અને $m$ હોય, તો ન્યુટનના ગુરુત્વાકર્ષણના નિયમ પરથી તેમની વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ $F = \frac{{GMm}}{{{r^2}}}$, જયાં $G =$ ગુરુત્વાકર્ષણનો અચળાંક છે. $G$ અને $K$ વચ્ચેનો સંબંઘ શેના વડે દર્શાવી શકાય?
- 10કોઈ સ્થાને ગુરુત્વાકર્ષણ ક્ષેત્ર $\overrightarrow g = 5\,N/kg\hat i\, + \,12\,N/kg\hat j$ મુજબા આપવામાં આવે છે.$1\, kg$ દળના પદાર્થને ઉગમબિંદુથી $(7\, m, - 3\, m)$ લઈ જતાં દળની ગુરુત્વસ્થિતિઊર્જામાં ....... $J$ ફેરફાર થાય.View Solution