(a) Radius of earth \(R = 6400\, km \)
\(h = \frac{R}{4}\) Acceleration due to gravity at a height h \({g_h} = g{\left( {\frac{R}{{R + h}}} \right)^2}\)
\( = g{\left( {\frac{R}{{R + \frac{R}{4}}}} \right)^2}\)
\( = \frac{{16}}{{25}}g\)
At depth \('d'\) value of acceleration due to gravity
\({g_d} = \frac{1}{2}{g_h}\) (According to problem)
\(⇒\) \({g_d} = \frac{1}{2}\left( {\frac{{16}}{{25}}} \right)g\) \( \Rightarrow g\left( {1 - \frac{d}{R}} \right)\)
\( = \frac{1}{2}\left( {\frac{{16}}{{25}}} \right)\;g\)
By solving we get \(d = 4.3 \times {10^6}\,m\)
Download our appand get started for free
Similar Questions
- 1View Solutionવિધાન : વાતાવરણ વગરની પૃથ્વી ખૂબ જ ઠંડી હોય.
કારણ : વાતાવરણ વગર બધી જ ઉષ્મા છટકી જાય.
- 2પૃથ્વીની ફરતે ફરતા ઉપગ્રહ માટે કુલ ઉર્જા ($E$) અને ગતિઉર્જા ($K$) અને સ્થિતિઉર્જા ($U$) નો ગ્રાફ નીચેની પૈકી ક્યો છે ?View Solution
- 3નીચેનામાંથી કોને સૌપ્રથમ $G$ નું પ્રાયોગિક મૂલ્ય આપ્યું?View Solution
- 4એક $90 \mathrm{~kg}$ ની વસ્તુને પૃથ્વીની સપાટીથી $2R$ અંતરે મૂકવામાં આવે છે કે જે. . . . . . . . . જેટલું ગુરુત્વાકર્ષી બળ અનુભવશે. $R$= પૃથ્વીની ત્રિજ્યા $\left.\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$View Solution
- 5નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $-I:$ પૃથ્વીની સપાટી પર અલગ અલગ સ્થાને ગુરુત્વ પ્રવેગનું મૂલ્ય અલગ અલગ હોય.
વિધાન $-II:$ પૃથ્વીની સપાટીની અંદર જતાં ગુરુત્વ પ્રવેગનું મૂલ્ય વધે છે.
ઉપરોક્ત વિધાનને અનુલક્ષીને આપેલ વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો
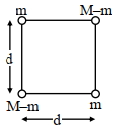
- 6$2 {M}$ દળના પદાર્થને ચાર $\{{m}, {M}-{m}, {m}, {M}-{m}\}$ દળના ટુકડામાં વિભાજિત કરીને આકૃતિમાં દર્શાવ્યા પ્રમાણે ચોરસમાં ગોઠવેલા છે. જ્યારે ગુરુત્વાકર્ષી સ્થિતિઉર્જા મહતમ હોય ત્યારે $\frac{{M}}{{m}}$ નો ગુણોત્તર ${x}: 1$ મળતો હોય તો $x$ નું મૂલ્ય કેટલું કેટલું હશે?View Solution
- 7દીર્ઘવૃતિય કક્ષામાં પરિભ્રમણ કરતા ગ્રહ માટે સૂર્યથી સૌથી નજીકનું અંતર $r_1$ અને સૌથી દૂરનું અંતર $r_2$ છે. જો $v_1$ અને $v_2$ એ અનુક્રમે આ બે બિંદુ આગળના રેખીય વેગ હોય, તો $\frac{v_1}{v_2}$ કેટલું થાય?View Solution
- 8એક ગ્રહનું દળ પૃથ્વીના દળ કરતાં $\frac{1}{10}$ (દસમા ભાગનું) અને તેનો વ્યાસ પૃથ્વી કરતાં અડધો છે. ગ્રહ ઉપર ગુરુત્વાકર્ષીય પ્રવેગ. . . . . . . હશે.View Solution
- 9એક સાદા લોલકનો આવર્તકાળ પૃથ્વીની સપાટી પર $T_1$ અને સપાટીથી $R$ ઊંચાઈએ $T_2$ હોય તો $T_2/T_1$ = _____ ($R=$ પૃથ્વીની ત્રિજ્યા)View Solution
- 10$g, R$ અને $G$ ના પદમાં પૃથ્વીના દળનું સૂત્ર શું થાય?View Solution
