As we know, Gravitational force of attraction,
\(F = \frac{{GMm}}{{{R^2}}}\)
\({F_1} = \frac{{G{M_e}m}}{{r_1^2}}\,and\,{F_2} = \frac{{G{m_e}{M_s}}}{{r_2^2}}\)
\(\Delta {F_1} = \frac{{2G{M_e}m}}{{r_1^3}}\Delta {r_1}\,and\,\Delta {F_2} = \frac{{G{M_e}{M_s}}}{{r_2^3}}\Delta {r_2}\)
\(\frac{{\Delta {F_1}}}{{\Delta {F_2}}} = \frac{{m\Delta {r_1}}}{{r_1^3}}\frac{{r_2^3}}{{{M_s}\Delta {r_2}}} = \left( {\frac{m}{{{M_s}}}} \right)\left( {\frac{{r_2^3}}{{r_1^3}}} \right)\left( {\frac{{\Delta {r_1}}}{{\Delta {r_2}}}} \right)\)
Using \(\Delta {r_1} = \Delta {r_2} = 2{R_{earth}};m = 8 \times {10^{22}}\,kg;\)
\({M_s} = 2 \times {10^{30\,}}kg\)
\({r_1} = 0.4 \times {10^6}km\,and\,{r_2} = 150 \times {10^6}\,km\)
\(\frac{{\Delta {F_1}}}{{\Delta {F_2}}} = \left( {\frac{{8 \times {{10}^{22}}}}{{2 \times {{10}^{30}}}}} \right){\left( {\frac{{150 \times {{10}^6}}}{{0.4 \times {{10}^6}}}} \right)^3} \times 1 \cong 2\)
Download our appand get started for free
Similar Questions
- 1એક ગોળાકાર ગ્રહનું દળ $M$ અને વ્યાસ $D$ છે. ગ્રહની સપાટીની નજીક કોઈ દળના કણ $m$ ને મુકત કરતાં તેના દ્વારા અનુભવાતો ગુરુત્વ પ્રવેગ કોને બરાબર થાય?View Solution
- 2પૃથ્વીની સપાટી પર પદાર્થનું વજન $72 \,N$ છે. જો તેને $h=2 R$ ઊંચાઈ એ લઈ જવામાં આવે, તો તેનું વજન ........... $N$ હશે ?View Solution
- 3$m$ દળના પદાર્થને પૃથ્વીની સપાટી પર મૂકેલો છે. તેને પૃથ્વીની સપાટીથી $h = 3R$ ઊંચાઇ પર લઈ જવામાં આવે છે. પદાર્થની ગુરુત્વ સ્થિતિઊર્જામાં થતો ફેરફાર કેટલો હશે?View Solution
- 4જો ${R}_{{E}}$ પૃથ્વીની ત્રિજ્યા હોય તો પૃથ્વીની સપાટીથી $r$ ઊંડાઈએ અને પૃથ્વીની સપાટીથી $r$ ઊંચાઈ પર ગુરુત્વપ્રવેગનો ગુણોત્તર કેટલો થાય? ($\left.{r}<{R}_{{E}}\right)$View Solution
- 5જો $R$ ત્રિજ્યા અને $M$ દળનાં ચંદ્રના કેન્દ્રથી $3 R$ અંતર $P$ બિંદુથી સ્થિર પદાર્થને મૂક્ત કરવામાં આવે છે. નીચે આપેલી કઈ ઝડપે પદાર્થને ચંદ્રને અથડાશે ?View Solution
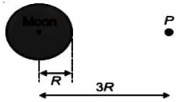
- 6ગ્રહની સૂર્યની આસપાસ ઉત્કેન્દ્રતા $e$ વાળી દીર્ધવૃત્તીય કક્ષામાં ગતિ દરમિયાન ચંદ્રનીચ અને ચંદ્રોચ્ય બિંદુએ ગતિઊર્જાનો ગુણોતર શું છે ?View Solution
- 7$m$ દળ ના પદાર્થ $X-$ અક્ષ પર $x = 1, x = 2, x = 4, x = 8$ …… સુઘી મૂકેલા છે.ઉદ્ગમબિંદુ $x = 0$ આગળ ગુરુત્વસ્થિતિમાન કેટલું થાય?View Solution
- 8View Solutionવિધાન : મુક્તપતન દરમિયાન જ્યારે અસરકારક રીતે પદાર્થનું વજન શૂન્ય થાય છે.
કારણ : મુક્તપતન દરમિયાન પદાર્થ પર લાગતુ ગુરુત્વપ્રવેગ શૂન્ય હોય
- 9ચંદ્રનું દળ એક ગ્રહના દળ કરતા $1 / 144$ ગણું અને તેનો વ્યાસ ગ્રહના વ્યાસ કરતા $1 / 16$ ગણુો છે. જો આપેલ ગ્રહ પર નિષ્ક્રમણ ઝડપ $\mathrm{v}$ હોય તો ચંદ્ર પર નિષ્કમાણ ઝડપ .........View Solution
- 10View Solutionસ્પેસશીપ માં રહેલા અવકાશયાત્રીને અવકાશ કેવું દેખાય ?
