As given in the first condition:
Both conducting spheres are shown.
\({V_{in}} - {V_{{\text{out }}}} = \left( {\frac{{{\text{kQ}}}}{{{r_1}}}} \right) - \left( {\frac{{{\text{kQ}}}}{{{{\text{r}}_2}}}} \right)\)
\( = {\text{kQ}}\left( {\frac{1}{{{{\text{r}}_1}}} - \frac{1}{{{{\text{r}}_2}}}} \right) = V\)
In the second condition:
Shell is now given charge \(-4 Q\)
\({V_{in}} - {V_{out}} = \left( {\frac{{kQ}}{{{r_1}}} - \frac{{4kQ}}{{{r_2}}}} \right) - \left( {\frac{{kQ}}{{{r_2}}} - \frac{{4kQ}}{{{r_2}}}} \right)\)
\( = \frac{{kQ}}{{{r_1}}} - \frac{{kQ}}{{{r_2}}}\)
\(=\mathrm{kQ}\left(\frac{1}{\mathrm{r}_{1}}-\frac{1}{\mathrm{r}_{2}}\right)=\mathrm{V}\)
Hence, we also obtain that potential difference does not depend on charge of outer sphere.
\(\therefore \) \(P.d.\) remains same.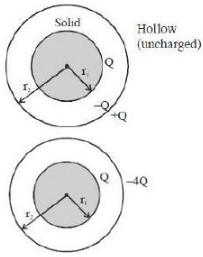
Download our appand get started for free
Similar Questions
- 1નીચે બે વિધાનો આપેેલા છે. એકને કથન $(A)$ અને બીજાને કારણ $(R)$ રજુ કરેલ છે.View Solution
કથન $(A):$ બે ધાત્વીય ગોળાઓને સમાન સ્થિતિમાનથી વીજભારિત કરવામાં આવેલ છે. તેમાનો એક પોલો અને બીજો ઘન છે, પરંતુ બંનેની ત્રિજ્યા સમાન છે. ઘન ગોળા પર પોલા ગોળા કરતા ઓછો વિદ્યુતભાર હશે.
કારણ $(R):$ ધાતુના ગોળાની સંઘારકતા ગોળાઓની ત્રિજ્યા ઉપર આધારિત છે.
ઉપરનાં વિધાનોનાં સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરો.
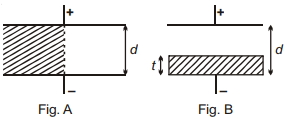
- 2એક સંધારકની (કેપેસીટર) બે પ્લેટો વચ્યેનું અંતર $d$ છે અને જ્યારે પ્લેટ વચ્ચે હવાનું માધ્યમ હોય ત્યારે તેની સંધારકતા (કેપેસીટન્સ) $C_1$ છે. જો $\frac{2d}{3}$ જાડાઈ અને પ્લેટોના જેટલા જ ક્ષેત્રફળ વાળી ધાતુની તકતીને પ્લેટોની વચ્યે દાખલ કરવામાં આવે, તો સંધારકની સંધારકતા $C_2$ થાય છે. $\frac{C_2}{C_1}$ નો ગુણોત્તર ...... છે.View Solution
- 3$14\, pF$ કેપેસિટરને $V =12\, V$ની બેટરી સાથે લગાવેલ છે.બેટરી દૂર કરીને ડાઇઇલેક્ટ્રીક $k =7$થી કેપેસિટરને ભરતા તેની ઊર્જામાં થતો ફેરફાર $..........pJ$ થાય.View Solution
- 4એક વિદ્યુત્ત દ્વિધ્રુવીને $1000 \,V/m$ વિદ્યુત્તક્ષેત્ર $45^o$ ના ખુણે આપવામાં આવે છે. વિદ્યુત દ્વિધ્રુવી ચાકમાત્રા $10^{-29}\,C.m$ છે. આપવામાં આવેલ વિદ્યુતક્ષેત્રની અસર હેઠળ વિદ્યુત દ્વિધ્રુવી ની સ્થિતિઉર્જા કેટલી હશે?View Solution
- 5$(-9\ cm, 0, 0)$ અને $(9\ cm, 0, 0)$ બિંદુ આગળ મૂકેલો બે વિદ્યુતભારો $7\ \mu C$ અને $-2 \ \mu C$ (અને બાહ્ય ક્ષેત્રની ગેરહાજરીમાં) વાળા તંત્રની સ્થિતિ વિદ્યુત સ્થિતિ ઊર્જા ગણો.........$J$View Solution
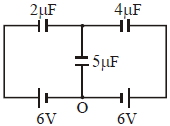
- 6આપેલ પરિપથમાં રહેલ $5\, \mu F$ કેપેસીટર પરનો વિજભાર $........\mu C$ હશે.View Solution
- 7$10\,\mu F$ ની સંઘારકતા ધરાવતા બે સમાંતર પ્લેટ સંઘારકો $C _1$ અને $C _2$ ને સ્વતંત્ર રીતે $100\,V\,D.C.$ ઉદગમથી વિદ્યુતભારિત કરવામાં આવે છે. સંઘારક $C _1$ ને ઉદગમ સાથે જોડેલા રાખીને તેની પ્લેટોની વચ્ચે અવાહક ચોસલું દાખલ કરવામાં આવે છે. સંઘારક $C _2$ એ ઉદગમથી છુટ્ટો કર્યા પછી તેની પ્લેટો વચ્ચે અવાહક ચોસલું દાખલ કરવામાં આવે છે. ત્યાર બાદ સંઘારક $C _1$ ને પણ ઉદગમથી છુટું કરી અંતમાં બંને સંઘારકોને સમાંતર જોડાણમાં જોડવામાં આવે છે. આ સંયોજનનું સામાન્ય સ્થિતિમાન $............\,V$ થશે.(ડાયઈલેક્ટ્રીક અચળાંક $=10$ છે તેમ ધારો)View Solution
- 8બે અલગ અલગ $\frac{2}{3} R$ અને $\frac{1}{3} R$ ત્રિજ્યા ધરાવતા $S_{1}$ અને $S_{2}$ વાહક ગોળા પર અનુક્રમે $12\, \mu C$ અને $-3\, \mu C$ જેટલો વિજભાર છે અને બંને એકબીજાથી ખૂબ જ લાંબા અંતરે છે. તેને હવે એક વાહક તારથી જોડેલા છે. તેના પછી લાંબા સમયે $S_{1}$ અને $S_{2}$ પરનો વિજભાર કેટલો હશે?View Solution
- 9$R$ ત્રિજ્યાની ધાત્વિય ગોળીય કવચના કેન્દ્રથી ત્રિજ્યાવર્તી અંતર $r$ નો વિધુતસ્થિતિમાન સાથેનો આલેખ નીચેનામાંથી ક્યો છે?View Solution
- 10આકૃતિમાં $A$ દર્શાવ્યા મુજબ એક કેપેસીટર ડાઈઈલેક્ટ્રીક ($K=2$) વડે અડધો ભરાયેલ છે. જો આકૃતિનાં બીજા ભાગ $B$ પ્રમાણે તે અડધો ભરાયેલ હોય તો ડાઈઈલેક્ટ્રીકની એવી જાડાઈ શોધો કે જેનાથી કેપેસીટરની ક્ષમતા એટલી જ રહે?View Solution