$R _1$ ત્રિજ્યાના અલગ કરેલા સંધારકની સંધારકતા $n$ ગણી વધી જાય છે જ્યારે તેને $R _2$ ત્રિજ્યા ધરાવતા અને પૃથ્વી સાથે જોડેલા $(grounded)$ સમકેન્દ્રીય ગોળામાં મૂકવામાં આવે છે. તેમની ત્રિજ્યાઆનો ગુણોત્તર $\left(\frac{R_2}{R_1}\right) \ldots$ થશે.
JEE MAIN 2022, Diffcult
a
Capacitance of isolated Conducting sphere \(=4 \pi \varepsilon_{0} R_{1}\)
Capacitance of isolated Conducting sphere \(=4 \pi \varepsilon_{0} R_{1}\)
By enclosing inside another sphere of radius \(R_{2}\), new capacitance \(=\frac{4 \pi \varepsilon_{0} R_{1} R_{2}}{\left(R_{2}-R_{1}\right)}\)
Given: \(\frac{4 \pi \varepsilon_{0} R_{1} R_{2}}{\left(R_{2}-R_{1}\right)}=n \times 4 \pi \varepsilon_{0} R_{1}\)
\(\frac{ R _{2}}{\left( R _{2}- R _{1}\right)}= n \Rightarrow \frac{\frac{ R _{2}}{ R _{1}}}{\left(\frac{ R _{2}}{ R _{1}}-1\right)}= n\)
\(\frac{ R _{2}}{ R _{1}}= n \frac{ R _{2}}{ R _{1}}- n \Rightarrow \frac{ R _{2}}{ R _{1}}=\frac{ n }{( n -1)}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બેટરીથી દૂર કરેલ એક કેપેસિટરનો કેપેસિટન્સ $C_o$ અને ઊર્જા $W_o$ અને છે.હવે ડાઇઇલેકિટ્રક અચલાંક $=$ $5$ ભરી દેતા નવોં કેપેસિટરનો કેપેસિટન્સ અને ઊર્જા કેટલી થાય?View Solution
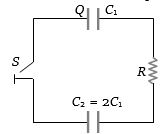
- 2જયારે કળ ખુલ્લી હોય,ત્યારે $C_1$ પર વિદ્યુતભાર $Q$ છે.જયારે કળ બંધ કરવામાં આવે,ત્યારે $C_1$ અને $C_2$ પર વિદ્યુતભાર કેટલો થાય?View Solution
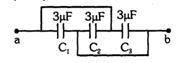
- 3આપેલા પરિપથમા $a$ અને $b$ વચ્ચે કેપેસિટન્સ ........$\mu F$ હશે.View Solution
- 4એક સંધારક $R$ અવરોધની મદદથી વિદ્યુતભાર રહિત (ડીસ્ચાર્જ) થાય છે. ધારો કે $t_{1}$ સમયમાં સંધારકમાં સંગ્રહીત ઊર્જા ધટીને તેની પ્રારંભિક મૂલ્ય કરતાં અડધી થાય છે અને $t _{2}$ સમયમાં સંગ્રહીત વિદ્યુતભાર ધટીને તેનાં પ્રારંભિક મૂલ્ય કરતા આઠમા ભાગનો થાય છે. $t_{1} / t_{2}$ ગુણોત્તર .............થશે.View Solution
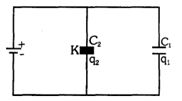
- 5આપેલ રેખાચિત્રમાં બે સમાન કેપેસિટર $C_1$ અને $C_2$ ને બેટરી સાથે જોડેલ છે. $C_1$ ની પ્લેટો વચ્ચે હવા વડે ભરવામાં આવે છે. અને $C_2$ વચ્ચેની પ્લેટો વચ્ચે અવાહક દ્રવ્યને ભરવામાંં આવે છે, તો,View Solution
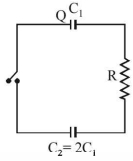
- 6આકૃતિમાં બતાવ્યા પ્રમાણે કેપેસિટરર $C _1$ અને $C _2=2 C _1$ ને તેમની વચ્ચે સ્વિય રહે તેમ પરિપથમાં જોંડલ છે. પ્રાંભમાં સ્વિચ ખુલ્લી છે અને વીજભાર $Q$ છે. $C _1$ પર સ્વીય બંધ છે. સ્થિર સ્થિતિમાં, દરેક કેપેસિટર પર વીજભાર $................$View Solution
- 7ગોળાકાર કેપેસિટરની ત્રિજ્યાઓ $0.5\, m$ અને $0.6\, m$ છે. જો ખાલી જગ્યાને $6$ ડાઈ ઈલેકટ્રીક અચળાંકના માધ્યમથી ભરવામાં આવે તો, કેપેસિટરની કેપેસિટિ કેટલી હશે ?View Solution
- 8સમાંતર પ્લેટ કેપેસિટરની પ્લેટો વચ્ચેના અવકાશમાં એકસમાન વિદ્યુતક્ષેત્ર $E$ છે. જો પ્લેટો વચ્ચેનું અંતર $d$ છે અને પ્લેટોનું ક્ષેત્રફળ $A$ હોય, તો કેપેસીટરમાં સંગ્રહ પામતી ઉર્જા કેટલી હશે?View Solution
- 9$200\,cm^2$ ક્ષેત્રફળ અને $1.5\,cm$ દૂર રાખેલી બે પ્લેટ સમાંતર પ્લેટ કેપેસીટર તરીકે વર્તે છે જેને $V\;emf$ જેટલી બેટરી સાથે જોડેલ છે. જો બંન્ને પ્લેટ વચ્ચે $25\times10^{-6}\,N$ જેટલું આકર્ષણબળ લાગતું હોય તો $V$ નું વોલ્ટમાં મૂલ્ય કેટલું હશે? $\left( {{\varepsilon _0} = 8.85 \times {{10}^{ - 12}}\,\frac{{{C^2}}}{{N{m^2}}}} \right)$View Solution
- 10પ્રોટોનનું દળ $1.67 \times 10^{-27} kg$ અને તેનો ચાર્જ $+1.6 \times 10^{-19} C$ છે. દસ લાખ વોલ્ટના વિદ્યુત સ્થિતિમાનનાં તફાવતે જો તેને પ્રવેગીત કરવામાં આવે તો તેની ગતિઊર્જા $\dots\dots J$ થશે.View Solution
